Interpreting the Central Limit Theorem In Exercises 19–26, find the mean and standard deviation of the indicated sampling distribution of sample means. Then sketch a graph of the sampling distribution.

Renewable Energy The zloty is the official currency of Poland. During a recent period of two years, the day-ahead prices for renewable energy in Poland (in zlotys per mega-watt hour) have a mean of 158.51 and a standard deviation of 33.424. Random samples of size 100 are drawn from this population, and the mean of each sample is determined. (Adapted from Multidisciplinary Digital Publishing Institute)

Interpreting the Central Limit Theorem In Exercises 19–26, find the mean and standard deviation of the indicated sampling distribution of sample means. Then sketch a graph of the sampling distribution.

Salaries The annual salaries for web software development managers are normally distributed, with a mean of about $136,000 and a standard deviation of about $11,500. Random samples of 40 are drawn from this population, and the mean of each sample is determined.

Repeat Exercise 26 for samples of size 72 and 108. What happens to the mean and the standard deviation of the distribution of sample means as the sample size increases?

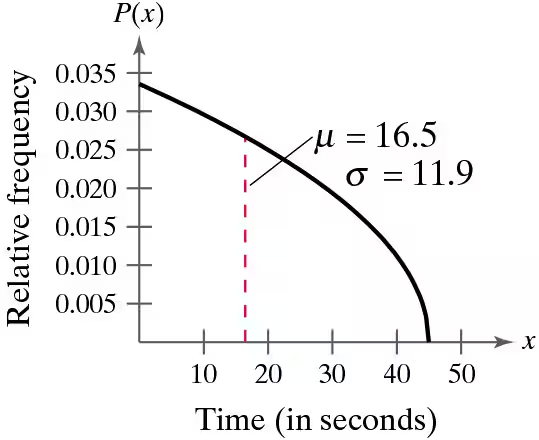
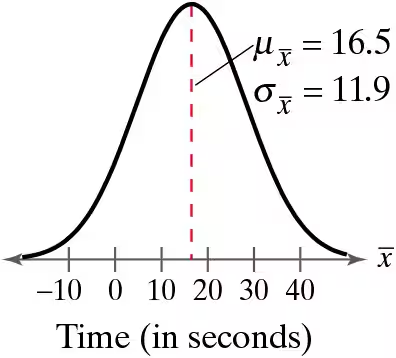
Graphical Analysis In Exercises 9 and 10, the graph of a population distribution is shown with its mean and standard deviation. Random samples of size 100 are drawn from the population. Determine which of the figures labeled (a)–(c) would most closely resemble the sampling distribution of sample means. Explain your reasoning.

The waiting time (in seconds) to turn left at an intersection

Construction About 63% of the residents in a town are in favor of building a new high school. One hundred five residents are randomly selected. What is the probability that the sample proportion in favor of building a new school is less than 55%? Interpret your result.

Paint Cans A machine is set to fill paint cans with a mean of 128 ounces and a standard deviation of 0.2 ounce. A random sample of 40 cans has a mean of 127.9 ounces. The machine needs to be reset when the mean of a random sample is unusual. Does the machine need to be reset? Explain.

Milk Containers A machine is set to fill milk containers with a mean of 64 ounces and a standard deviation of 0.11 ounce. A random sample of 40 containers has a mean of 64.05 ounces. The machine needs to be reset when the mean of a random sample is unusual. Does the machine need to be reset? Explain.

Conservation About 74% of the residents in a town say that they are making an effort to conserve water or electricity. One hundred ten residents are randomly selected. What is the probability that the sample proportion making an effort to conserve water or electricity is greater than 80%? Interpret your result.

Employee Wellness A survey of employed U.S. adults found that only 35% believe their employer cares about their well-being. You randomly select a sample of U.S. employees. Find the probability that fewer than 100 believe their employer cares about their well-being. (Source: Gallup)

c. You select 400 U.S. employees.

Daily Commute About 83% of U.S. employees drive their own vehicle to work. You randomly select a sample of U.S. employees. Find the probability that more than 100 of the employees drive their own vehicle to work. (Source: U.S. Bureau of Labor Statistics)

c. You select 150 U.S. employees.

Approximating a Binomial Distribution In Exercises 17 and 18, a binomial experiment is given. Determine whether you can use a normal distribution to approximate the binomial distribution. If you can, find the mean and standard deviation. If you cannot, explain why.

Bachelor’s Degrees Twenty-two percent of adults over 18 years of age have a bachelor’s degree. You randomly select 20 adults over 18 years of age and ask whether they have a bachelor’s degree.

In Exercises 1–4, the sample size n, probability of success p, and probability of failure q are given for a binomial experiment. Determine whether you can use a normal distribution to approximate the distribution of x.

n=18, p=0.90, q=0.10

In Exercises 5–8, match the binomial probability statement with its corresponding normal distribution probability statement (a)–(d) after a continuity correction.

P(x≥109)

a. P(x>109.5)

b. P(x<108.5)

c. P(x<109.5)

d. P(x>108.5)

In Exercises 9–14, write the binomial probability in words. Then, use a continuity correction to convert the binomial probability to a normal distribution probability.

P(x ≥ 110)

In Exercises 9–14, write the binomial probability in words. Then, use a continuity correction to convert the binomial probability to a normal distribution probability.

P(x > 65)

In Exercises 9–14, write the binomial probability in words. Then, use a continuity correction to convert the binomial probability to a normal distribution probability.

P(x ≤ 150)

In Exercises 9–14, write the binomial probability in words. Then, use a continuity correction to convert the binomial probability to a normal distribution probability.

P(55 < x < 60)

In Exercises 1–4, the sample size n, probability of success p, and probability of failure q are given for a binomial experiment. Determine whether you can use a normal distribution to approximate the distribution of x.

n=24, p=0.85, q=0.15

In Exercises 1–4, the sample size n, probability of success p, and probability of failure q are given for a binomial experiment. Determine whether you can use a normal distribution to approximate the distribution of x.

n=20, p=0.65, q=0.35

In Exercises 5–8, match the binomial probability statement with its corresponding normal distribution probability statement (a)–(d) after a continuity correction.

P(x<109)

a. P(x>109.5)

b. P(x<108.5)

c. P(x<109.5)

d. P(x>108.5)

Approximating Binomial Probabilities In Exercises 19–26, determine whether you can use a normal distribution to approximate the binomial distribution. If you can, use the normal distribution to approximate the indicated probabilities and sketch their graphs. If you cannot, explain why and use a binomial distribution to find the indicated probabilities. Identify any unusual events. Explain.

Social Media A survey of Americans found that 55% would be disappointed if Facebook disappeared. You randomly select 500 Americans and ask them whether they would be disappointed if Facebook disappeared. Find the probability that the number who say yes is (a) less than 250

Approximating Binomial Probabilities In Exercises 19–26, determine whether you can use a normal distribution to approximate the binomial distribution. If you can, use the normal distribution to approximate the indicated probabilities and sketch their graphs. If you cannot, explain why and use a binomial distribution to find the indicated probabilities. Identify any unusual events. Explain.

Social Media A survey of Americans found that 55% would be disappointed if Facebook disappeared. You randomly select 500 Americans and ask them whether they would be disappointed if Facebook disappeared. Find the probability that the number who say yes is (b) at least 300

Approximating Binomial Probabilities In Exercises 19–26, determine whether you can use a normal distribution to approximate the binomial distribution. If you can, use the normal distribution to approximate the indicated probabilities and sketch their graphs. If you cannot, explain why and use a binomial distribution to find the indicated probabilities. Identify any unusual events. Explain.

Social Media A survey of Americans found that 55% would be disappointed if Facebook disappeared. You randomly select 500 Americans and ask them whether they would be disappointed if Facebook disappeared. Find the probability that the number who say yes is (c) between 240 and 280, inclusive.

Approximating Binomial Probabilities In Exercises 19–26, determine whether you can use a normal distribution to approximate the binomial distribution. If you can, use the normal distribution to approximate the indicated probabilities and sketch their graphs. If you cannot, explain why and use a binomial distribution to find the indicated probabilities. Identify any unusual events. Explain.

Athletes on Social Issues In a survey of college athletes, 84% said they are willing to speak up and be more active in social issues. You randomly select 25 college athletes. Find the probability that the number who are willing to speak up and be more active in social issues is (a) at least 24

Approximating Binomial Probabilities In Exercises 19–26, determine whether you can use a normal distribution to approximate the binomial distribution. If you can, use the normal distribution to approximate the indicated probabilities and sketch their graphs. If you cannot, explain why and use a binomial distribution to find the indicated probabilities. Identify any unusual events. Explain.

Athletes on Social Issues In a survey of college athletes, 84% said they are willing to speak up and be more active in social issues. You randomly select 25 college athletes. Find the probability that the number who are willing to speak up and be more active in social issues is (b) less than 23

Approximating Binomial Probabilities In Exercises 19–26, determine whether you can use a normal distribution to approximate the binomial distribution. If you can, use the normal distribution to approximate the indicated probabilities and sketch their graphs. If you cannot, explain why and use a binomial distribution to find the indicated probabilities. Identify any unusual events. Explain.

Athletes on Social Issues In a survey of college athletes, 84% said they are willing to speak up and be more active in social issues. You randomly select 25 college athletes. Find the probability that the number who are willing to speak up and be more active in social issues is (c) between 18 and 22, inclusive.

Approximating Binomial Probabilities In Exercises 19–26, determine whether you can use a normal distribution to approximate the binomial distribution. If you can, use the normal distribution to approximate the indicated probabilities and sketch their graphs. If you cannot, explain why and use a binomial distribution to find the indicated probabilities. Identify any unusual events. Explain.

Advancing Research In a survey of U.S. adults, 77% said are willing to share their personal health information to advance medical research. You randomly select 500 U.S. adults. Find the probability that the number who are willing to share their personal health information to advance medical research is (a) at most 400

Approximating Binomial Probabilities In Exercises 19–26, determine whether you can use a normal distribution to approximate the binomial distribution. If you can, use the normal distribution to approximate the indicated probabilities and sketch their graphs. If you cannot, explain why and use a binomial distribution to find the indicated probabilities. Identify any unusual events. Explain.

Advancing Research In a survey of U.S. adults, 77% said are willing to share their personal health information to advance medical research. You randomly select 500 U.S. adults. Find the probability that the number who are willing to share their personal health information to advance medical research is (b) more than 360

Approximating Binomial Probabilities In Exercises 19–26, determine whether you can use a normal distribution to approximate the binomial distribution. If you can, use the normal distribution to approximate the indicated probabilities and sketch their graphs. If you cannot, explain why and use a binomial distribution to find the indicated probabilities. Identify any unusual events. Explain.

Advancing Research In a survey of U.S. adults, 77% said are willing to share their personal health information to advance medical research. You randomly select 500 U.S. adults. Find the probability that the number who are willing to share their personal health information to advance medical research is (c) between 380 and 390 inclusive.

Testing a Drug A drug manufacturer claims that a drug cures a rare skin disease 75% of the time. The claim is checked by testing the drug on 100 patients. If at least 70 patients are cured, then this claim will be accepted. Use this information in Exercises 31 and 32.

Find the probability that the claim will be accepted, assuming that the actual probability that the drug cures the skin disease is 65%.