Back
BackProblem 5.R.56c
In Exercises 55–60, find the indicated probabilities and interpret the results.
Refer to Exercise 34. A random sample of six days is selected. Find the probability that the mean surface concentration of carbonyl sulfide for the sample is (c) more than 11.1 picomoles per liter. Compare your answers with those in Exercise 34.
Problem 5.R.57c
In Exercises 55–60, find the indicated probabilities and interpret the results.
The mean ACT composite score in a recent year is 20.7. A random sample of 36 ACT composite scores is selected. What is the probability that the mean score for the sample is (c) between 20 and 21.5? Assume σ=5.9.
Problem 5.R.58b
In Exercises 55–60, find the indicated probabilities and interpret the results.
The mean MCAT total score in a recent year is 500.9. A random sample of 32 MCAT total scores is selected. What is the probability that the mean score for the sample is (b) more than 502? Assume sigma=10.6.
Problem 5.RS.2b
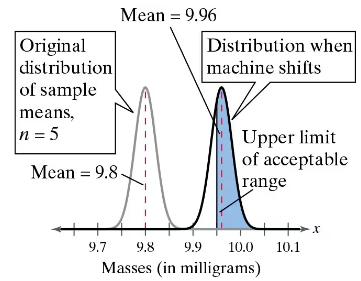
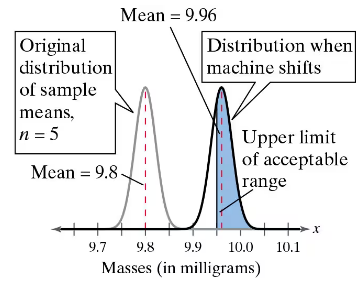
Assume the machine shifts and is filling the vials with a mean amount of 9.96 milligrams and a standard deviation of 0.05 milligram. You select five vials and find the mean amount of compound added.
b. You randomly select three samples of five vials. What is the probability that you select at least one sample of five vials that has a mean that is within the acceptable range?
Problem 5.RS.2c
Assume the machine shifts and is filling the vials with a mean amount of 9.96 milligrams and a standard deviation of 0.05 milligram. You select five vials and find the mean amount of compound added.
c. Which is more sensitive to a shift of parameters—an individual random selection or a randomly selected sample mean?
Problem 5.T.6
Use technology to find the standard deviation of the set of 36 sample means. How does it compare with the standard deviation of the ages found in Exercise 5? Does this agree with the result predicted by the Central Limit Theorem?
Problem 5.CR.15b
The initial pressures for bicycle tires when first filled are normally distributed, with a mean of 70 pounds per square inch (psi) and a standard deviation of 1.2 psi.
b. A random sample of 15 tires is drawn from this population. What is the probability that the mean tire pressure of the sample is less than 69 psi?
Problem 5.R.59b
In Exercises 55–60, find the indicated probabilities and interpret the results.
The mean annual salary for Level 1 actuaries in the United States is about $72,000. A random sample of 45 Level 1 actuaries is selected. What is the probability that the mean annual salary of the sample is (b) more than $68,000? Assume sigma = $11,000.
Problem 5.R.60b
In Exercises 55–60, find the indicated probabilities and interpret the results.
The mean annual salary for physical therapists in the United States is about $87,000. A random sample of 50 physical therapists is selected. What is the probability that the mean annual salary of the sample is (b) more than $85,000? Assume sigma = $10,500.
Problem 5.T.5a
In Exercises 5 and 6, determine whether you can use a normal distribution to approximate the binomial distribution. If you can, use the normal distribution to approximate the indicated probabilities and sketch their graphs. If you cannot, explain why and use a binomial distribution to find the indicated probabilities.
A survey of U.S. undergraduates found that 37% of those attending in-state colleges would prefer to take a job in a different state after graduation. You randomly select 18 U.S. undergraduates attending in-state colleges. Find the probability that the number who would prefer to take a job in a different state after graduation is (a) exactly 7. Identify any unusual events. Explain.
Problem 5.T.3b
In Exercises 5 and 6, determine whether you can use a normal distribution to approximate the binomial distribution. If you can, use the normal distribution to approximate the indicated probabilities and sketch their graphs. If you cannot, explain why and use a binomial distribution to find the indicated probabilities.
A survey of U.S. undergraduates found that 37% of those attending in-state colleges would prefer to take a job in a different state after graduation. You randomly select 18 U.S. undergraduates attending in-state colleges. Find the probability that the number who would prefer to take a job in a different state after graduation is (b) less than 5. Identify any unusual events. Explain.
Problem 5.T.1b
A certain stock's daily percent return on Fridays has a mean of 3.12% and a standard deviation of 41.25%. If random samples of 40 days are selected and the mean return for each sample is calculated, what is the probability that a sample mean is greater than 17%?
Problem 5.T.1c
During a recent period of one year, the mean percent increase in value on Wednesdays of the cryptocurrency Dogecoin was 7.46%, with a standard deviation of 53.47%. Random samples of size 50 are drawn from this population and the mean of each sample is determined. (Source: Crypto Indicators)
c. What is the probability that the mean percent increase for a given sample is between −10% and 30%?
Problem 5.1.26
Finding Area
In Exercises 23–36, find the indicated area under the standard normal curve. If convenient, use technology to find the area.
To the left of z=1.365
Problem 5.1.37a
Manufacturer Claims You work for a consumer watchdog publication and are testing the advertising claims of a tire manufacturer. The manufacturer claims that the life spans of the tires are normally distributed, with a mean of 40,000 miles and a standard deviation of 4000 miles. You test 16 tires and record the life spans shown below.
a. Draw a frequency histogram to display these data. Use five classes. Do the life spans appear to be normally distributed? Explain.
Problem 5.1.38a
[APPLET] Milk Consumption You are performing a study about weekly per capita milk consumption. A previous study found weekly per capita milk consumption to be normally distributed, with a mean of 48.7 fluid ounces and a standard deviation of 8.6 fluid ounces. You randomly sample 30 people and record the weekly milk consumptions shown below.
a. Draw a frequency histogram to display these data. Use seven classes. Do the consumptions appear to be normally distributed? Explain.
Problem 5.1.8
Explain how to transform a given x-value of a normally distributed variable x into a z-score.
Problem 5.1.39
Computing and Interpreting z-Scores In Exercises 39 and 40, (a) find the z-score that corresponds to each value and (b) determine whether any of the values are unusual.
Stanford-Binet IQ Scores The test scores for the Stanford-Binet Intelligence Scale are normally distributed with a mean score of 100 and a standard deviation of 16. The test scores of four students selected at random are 98, 65, 106, and 124.
Problem 5.1.35
Finding Area In Exercises 23–36, find the indicated area under the standard normal curve. If convenient, use technology to find the area.
To the left of z= -1.28 and to the right of z= 1.28
Problem 5.1.48
Finding Probability In Exercises 47–56, find the indicated probability using the standard normal distribution. If convenient, use technology to find the probability.
P(z < - 1.11)
Problem 5.1.1
Given the mean of a normal distribution, how can you find the median?
Problem 5.1.3
Describe the inflection points on the graph of a normal distribution. At what x-values are the inflection points located?
Problem 5.1.5
Draw two normal curves that have the same mean but different standard deviations. Describe the similarities and differences.
Problem 5.1.51
Finding Probability In Exercises 47–56, find the indicated probability using the standard normal distribution. If convenient, use technology to find the probability.
P(- 0.89 < z < 0)
Problem 5.1.54
Finding Probability In Exercises 47–56, find the indicated probability using the standard normal distribution. If convenient, use technology to find the probability.
P(- 1.54 < z < 1.54)
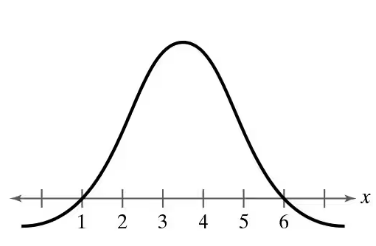
Problem 5.1.11
Graphical Analysis In Exercises 11–16, determine whether the graph could represent a variable with a normal distribution. Explain your reasoning. If the graph appears to represent a normal distribution, estimate the mean and standard deviation.
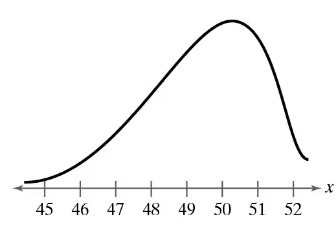
Problem 5.1.14
Graphical Analysis In Exercises 11–16, determine whether the graph could represent a variable with a normal distribution. Explain your reasoning. If the graph appears to represent a normal distribution, estimate the mean and standard deviation.
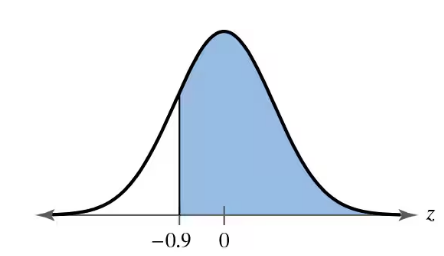
Problem 5.1.17
Using and Interpreting Concepts
Finding Area In Exercises 17–22, find the area of the shaded region under the standard normal curve. If convenient, use technology to find the area.
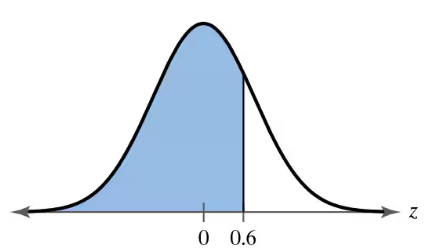
Problem 5.1.20
Using and Interpreting Concepts
Finding Area In Exercises 17–22, find the area of the shaded region under the standard normal curve. If convenient, use technology to find the area.
Problem 5.1.23
Finding Area
In Exercises 23–36, find the indicated area under the standard normal curve. If convenient, use technology to find the area.
To the left of z=0.33