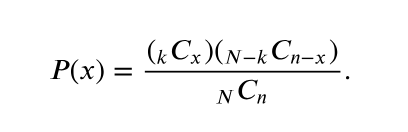Using a Distribution to Find Probabilities In Exercises 11–26, find the indicated probabilities using the geometric distribution, the Poisson distribution, or the binomial distribution. Then determine whether the events are unusual. If convenient, use a table or technology to find the probabilities.

Pass Completions NFL player Aaron Rodgers completes a pass 65.1% of the time. Find the probability that (a) the first pass he completes is the second pass, (b) the first pass he completes is the first or second pass, and (c) he does not complete his first two passes. (Source: National Football League)

Using a Distribution to Find Probabilities In Exercises 11–26, find the indicated probabilities using the geometric distribution, the Poisson distribution, or the binomial distribution. Then determine whether the events are unusual. If convenient, use a table or technology to find the probabilities.

Living Donor Transplants The mean number of organ transplants from living donors performed per day in the United States in 2020 was about 16. Find the probability that the number of organ transplants from living donors performed on any given day is (a) exactly 12 (Source: Organ Procurement and Transplantation Network)

Using a Distribution to Find Probabilities In Exercises 11–26, find the indicated probabilities using the geometric distribution, the Poisson distribution, or the binomial distribution. Then determine whether the events are unusual. If convenient, use a table or technology to find the probabilities.

Living Donor Transplants The mean number of organ transplants from living donors performed per day in the United States in 2020 was about 16. Find the probability that the number of organ transplants from living donors performed on any given day is (b) at least eight (Source: Organ Procurement and Transplantation Network)

Using a Distribution to Find Probabilities In Exercises 11–26, find the indicated probabilities using the geometric distribution, the Poisson distribution, or the binomial distribution. Then determine whether the events are unusual. If convenient, use a table or technology to find the probabilities.

Living Donor Transplants The mean number of organ transplants from living donors performed per day in the United States in 2020 was about 16. Find the probability that the number of organ transplants from living donors performed on any given day is (c) no more than 10. (Source: Organ Procurement and Transplantation Network)

Using a Distribution to Find Probabilities In Exercises 11–26, find the indicated probabilities using the geometric distribution, the Poisson distribution, or the binomial distribution. Then determine whether the events are unusual. If convenient, use a table or technology to find the probabilities.

Oil Tankers In the month of June 2021, 240 oil tankers stop at a port city. No oil tanker visits more than once. Find the probability that the number of oil tankers that stop on any given day in June is (a) exactly eight

Using a Distribution to Find Probabilities In Exercises 11–26, find the indicated probabilities using the geometric distribution, the Poisson distribution, or the binomial distribution. Then determine whether the events are unusual. If convenient, use a table or technology to find the probabilities.

Oil Tankers In the month of June 2021, 240 oil tankers stop at a port city. No oil tanker visits more than once. Find the probability that the number of oil tankers that stop on any given day in June is (b) at most three

Using a Distribution to Find Probabilities In Exercises 11–26, find the indicated probabilities using the geometric distribution, the Poisson distribution, or the binomial distribution. Then determine whether the events are unusual. If convenient, use a table or technology to find the probabilities.

Oil Tankers In the month of June 2021, 240 oil tankers stop at a port city. No oil tanker visits more than once. Find the probability that the number of oil tankers that stop on any given day in June is (c) more than eight.

Hypergeometric Distribution Binomial experiments require that any sampling be done with replacement because each trial must be independent of the others. The hypergeometric distribution also has two outcomes: success and failure. The sampling, however, is done without replacement. For a population of N items having k successes and failures, the probability of selecting a sample of size that has successes and failures is given by

In a shipment of 15 microchips, 2 are defective and 13 are not defective. A sample of three microchips is chosen at random. Use the above formula to find the probability that (a) all three microchips are not defective

Hypergeometric Distribution Binomial experiments require that any sampling be done with replacement because each trial must be independent of the others. The hypergeometric distribution also has two outcomes: success and failure. The sampling, however, is done without replacement. For a population of N items having k successes and failures, the probability of selecting a sample of size that has successes and failures is given by

In a shipment of 15 microchips, 2 are defective and 13 are not defective. A sample of three microchips is chosen at random. Use the above formula to find the probability that (b) one microchip is defective and two are not defective

Hypergeometric Distribution Binomial experiments require that any sampling be done with replacement because each trial must be independent of the others. The hypergeometric distribution also has two outcomes: success and failure. The sampling, however, is done without replacement. For a population of N items having k successes and failures, the probability of selecting a sample of size that has successes and failures is given by

In a shipment of 15 microchips, 2 are defective and 13 are not defective. A sample of three microchips is chosen at random. Use the above formula to find the probability that (c) two microchips are defective and one is not defective.

"Using a Distribution to Find Probabilities In Exercises 11–26, find the indicated probabilities using the geometric distribution, the Poisson distribution, or the binomial distribution. Then determine whether the events are unusual. If convenient, use a table or technology to find the probabilities.

Hurricanes The mean number of hurricanes to strike the U.S. mainland per year from 1851 through 2020 was about 1.8. Find the probability that the number of hurricanes striking the U.S. mainland in any given year from 1851 through 2020 is (a) exactly one, (b) at most one, and (c) more than one. (Source: National Oceanic & Atmospheric Administration)"

"Using a Distribution to Find Probabilities In Exercises 11–26, find the indicated probabilities using the geometric distribution, the Poisson distribution, or the binomial distribution. Then determine whether the events are unusual. If convenient, use a table or technology to find the probabilities.

Typographical Errors A newspaper finds that the mean number of typographical errors per page is four. Find the probability that the number of typographical errors found on any given page is (a) exactly three, (b) at most three, and (c) more than three."