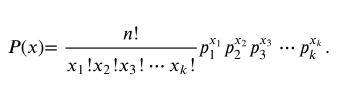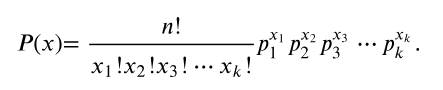Back
BackProblem 4.1.25
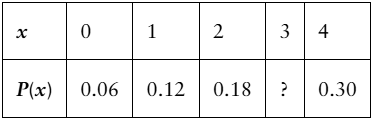
Determining a Missing Probability In Exercises 25 and 26, determine the missing probability for the probability distribution.
Problem 4.1.26
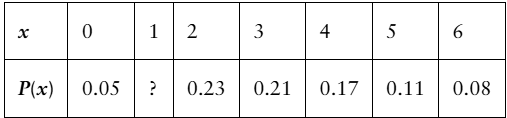
Determining a Missing Probability In Exercises 25 and 26, determine the missing probability for the probability distribution.
Problem 4.1.27
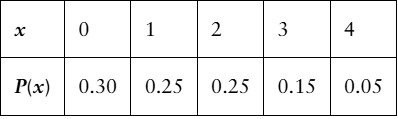
Identifying Probability Distributions In Exercises 27 and 28, determine whether the distribution is a probability distribution. If it is not a probability distribution, explain why.
Problem 4.1.7
"True or False? In Exercises 5–8, determine whether the statement is true or false. If it is false, rewrite it as a true statement.
The mean of the random variable of a probability distribution describes how the outcomes vary."
Problem 4.2.3
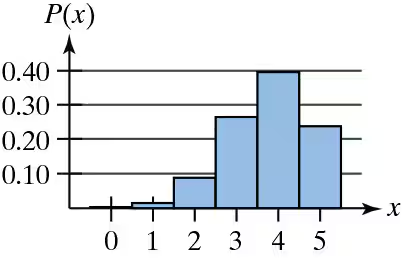
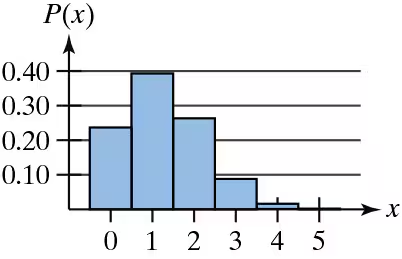
Graphical Analysis In Exercises 3–5, the histogram represents a binomial distribution with five trials. Match the histogram with the appropriate probability of success p. Explain your reasoning.
a. p = 0.25
b. p = 0.50
c. p = 0.75
Problem 4.2.5
Graphical Analysis In Exercises 3–5, the histogram represents a binomial distribution with five trials. Match the histogram with the appropriate probability of success p. Explain your reasoning.
a. p = 0.25
b. p = 0.50
c. p = 0.75
Problem 4.2.41b
Manufacturing An assembly line produces 10,000 automobile parts. Twenty percent of the parts are defective. An inspector randomly selects 10 of the parts
b. Because the sample is only 0.1% of the population, treat the events as independent and use the binomial probability formula to approximate the probability that none of the selected parts are defective.
Problem 4.2.41a
Manufacturing An assembly line produces 10,000 automobile parts. Twenty percent of the parts are defective. An inspector randomly selects 10 of the parts
a. Use the Multiplication Rule (discussed in Section 3.2) to find the probability that none of the selected parts are defective. (Note that the events are dependent.)
Problem 4.2.37a
Unusual Events In Exercises 37 and 38, find the indicated probabilities. Then determine if the event is unusual. Explain your reasoning.
Rock-Paper-Scissors The probability of winning a game of rock-paper-scissors is 1/3. You play nine games of rock-paper-scissors. Find the probability that the number of games you win is (a) exactly five
Problem 4.2.27
Constructing and Graphing Binomial Distributions In Exercises 27–30, (a) construct a binomial distribution, (b) graph the binomial distribution using a histogram and describe its shape, and (c) identify any values of the random variable x that you would consider unusual. Explain your reasoning.
College Acceptance Pennsylvania State University accepts 49% of applicants. You randomly select seven Pennsylvania State University applicants. The random variable represents the number who are accepted. (Source: US News & World Report)
Problem 4.2.30
Constructing and Graphing Binomial Distributions In Exercises 27–30, (a) construct a binomial distribution, (b) graph the binomial distribution using a histogram and describe its shape, and (c) identify any values of the random variable x that you would consider unusual. Explain your reasoning.
Workplace Cleanliness Fifty-seven percent of employees judge their peers by the cleanliness of their workspaces. You randomly select 10 employees and ask them whether they judge their peers by the cleanliness of their workspaces. The random variable represents the number who judge their peers by the cleanliness of their workspaces. (Source: Adecco)
Problem 4.2.11
Mean, Variance, and Standard Deviation In Exercises 11–14, find the mean, variance, and standard deviation of the binomial distribution with the given values of n and p.
n = 50, p = 0.4
Problem 4.2.14
Mean, Variance, and Standard Deviation In Exercises 11–14, find the mean, variance, and standard deviation of the binomial distribution with the given values of n and p.
n = 316, p = 0.82
Problem 4.2.37b
Unusual Events In Exercises 37 and 38, find the indicated probabilities. Then determine if the event is unusual. Explain your reasoning.
Rock-Paper-Scissors The probability of winning a game of rock-paper-scissors is 1/3. You play nine games of rock-paper-scissors. Find the probability that the number of games you win is (b) more than five
Problem 4.2.37c
Unusual Events In Exercises 37 and 38, find the indicated probabilities. Then determine if the event is unusual. Explain your reasoning.
Rock-Paper-Scissors The probability of winning a game of rock-paper-scissors is 1/3. You play nine games of rock-paper-scissors. Find the probability that the number of games you win is (c) less than two.
Problem 4.2.24
Finding Binomial Probabilities In Exercises 19–26, find the indicated probabilities. If convenient, use technology or Table 2 in Appendix B.
Responsible Consumption Forty-five percent of consumers say it is important that the clothing they buy is made without child labor. You randomly select 16 consumers. Find the probability that the number of of consumers who say it is important that the clothing they buy is made without child labor is (a) e
Problem 4.2.22
Finding Binomial Probabilities In Exercises 19–26, find the indicated probabilities. If convenient, use technology or Table 2 in Appendix B.
Penalty Kicks Argentine soccer player Lionel Messi converts 78% of his penalty kicks. Suppose Messi takes six penalty kicks next season. Find the probability that the number he converts is (a) exactly six, (b) at most three, and (c) more than three. (Source: Transfermarkt)
Problem 4.2.20
Finding Binomial Probabilities In Exercises 19–26, find the indicated probabilities. If convenient, use technology or Table 2 in Appendix B.
Civil Rights Fifty-nine percent of U.S. adults think that civil rights for Black Americans have improved during their lifetime. You randomly select seven U.S. adults. Find the probability that the number who think that civil rights for Black Americans have improved during their lifetime is (a) exactly one and (b) exactly five. (Source: Gallup)
Problem 4.2.18
Identifying and Understanding Binomial Experiments In Exercises 15–18, determine whether the experiment is a binomial experiment. If it is, identify a success; specify the values of n, p, and q; and list the possible values of the random variable x. If it is not a binomial experiment, explain why.
Basketball A’ja Wilson, the 2020 WNBA Most Valuable Player, makes a free throw shot about 78% of the time. The random variable represents the number of free throws that she makes on eight attempts. (Source: Women’s National Basketball Association)
Problem 4.2.15
Identifying and Understanding Binomial Experiments In Exercises 15–18, determine whether the experiment is a binomial experiment. If it is, identify a success; specify the values of n, p, and q; and list the possible values of the random variable x. If it is not a binomial experiment, explain why.
Video Games A survey found that 29% of gamers own a virtual reality (VR) device. Ten gamers are randomly selected. The random variable represents the number who own a VR device. (Source: Entertainment Software Association)
Problem 4.2.39
Multinomial Experiments In Exercises 39 and 40, use the information below.
A multinomial experiment satisfies these conditions.
The experiment has a fixed number of trials n, where each trial is independent of the other trials.
Each trial has k possible mutually exclusive outcomes:
Each outcome has a fixed probability. So, . The sum of the probabilities for all outcomes is
The number of times occurs is , the number of times occurs is , the number of times occurs is , and so on.
The discrete random variable x counts the number of times that each outcome occurs in n independent trials where . The probability that x will occur is
Genetics According to a theory in genetics, when tall and colorful plants are crossed with short and colorless plants, four types of plants will result: tall and colorful, tall and colorless, short and colorful, and short and colorless, with corresponding probabilities of , and . Ten plants are selected. Find the probability that 5 will be tall and colorful, 2 will be tall and colorless, 2 will be short and colorful, and 1 will be short and colorless.
Problem 4.2.33
Finding and Interpreting Mean, Variance, and Standard Deviation In Exercises 31–36, find the mean, variance, and standard deviation of the binomial distribution for the given random variable. Interpret the results and determine any unusual values.
Life on Other Planets Seventy-nine percent of U.S. adults believe that life on other planets is plausible. You randomly select eight U.S. adults and ask them whether they believe that life on other planets is plausible. The random variable represents the number who believe that life on other planets is plausible. (Source: Ipsos)
Problem 4.2.35
Finding and Interpreting Mean, Variance, and Standard Deviation In Exercises 31–36, find the mean, variance, and standard deviation of the binomial distribution for the given random variable. Interpret the results and determine any unusual values.
Late for Work Thirty-one percent of U.S. employees who are late for work blame oversleeping. You randomly select 12 U.S. employees who are late for work and ask them whether they blame oversleeping. The random variable represents the number who are late for work and blame oversleeping. (Source: CareerBuilder)
Problem 4.2.40
"Multinomial Experiments In Exercises 39 and 40, use the information below.
A multinomial experiment satisfies these conditions.
The experiment has a fixed number of trials n, where each trial is independent of the other trials.
Each trial has k possible mutually exclusive outcomes:
Each outcome has a fixed probability. So, . The sum of the probabilities for all outcomes is
The number of times occurs is , the number of times occurs is , the number of times occurs is , and so on.
The discrete random variable x counts the number of times that each outcome occurs in n independent trials where . The probability that x will occur is
Genetics Another proposed theory in genetics gives the corresponding probabilities for the four types of plants described in Exercise 39 as , and . Ten plants are selected. Find the probability that 5 will be tall and colorful, 2 will be tall and colorless, 2 will be short and colorful, and 1 will be short and colorless."
Problem 4.3.10
In your own words, describe the difference between the value of x in a binomial distribution and in the Poisson distribution.
Problem 4.3.1
In Exercises 1– 4, find the indicated probability using the geometric distribution.
Find P(3) when p = 0.65
Problem 4.3.3
In Exercises 1– 4, find the indicated probability using the geometric distribution.
Find P(5) when p = 0.09
Problem 4.3.6
In Exercises 5–8, find the indicated probability using the Poisson distribution.
P(3) when μ = 6
Problem 4.3.30
Geometric Distribution: Mean and Variance In Exercises 29 and 30, use the fact that the mean of a geometric distribution is μ = 1/p and the variance is
sigma^2 = q/p^2
Paycheck Errors A company assumes that 0.5% of the paychecks for a year were calculated incorrectly. The company has 200 employees and examines the payroll records from one month. (a) Find the mean, variance, and standard deviation. (b) How many employee payroll records would you expect to examine before finding one with an error?
Problem 4.3.12
Using a Distribution to Find Probabilities In Exercises 11–26, find the indicated probabilities using the geometric distribution, the Poisson distribution, or the binomial distribution. Then determine whether the events are unusual. If convenient, use a table or technology to find the probabilities.
Immigration The mean number of people who immigrated to the United States per hour was about 5.5 in April 2021. Find the probability that the number of people who immigrate to the U.S. in a given hour in April 2021 was (a) zero, (b) exactly five, and (c) exactly eight. (Source: U.S. Census Bureau)