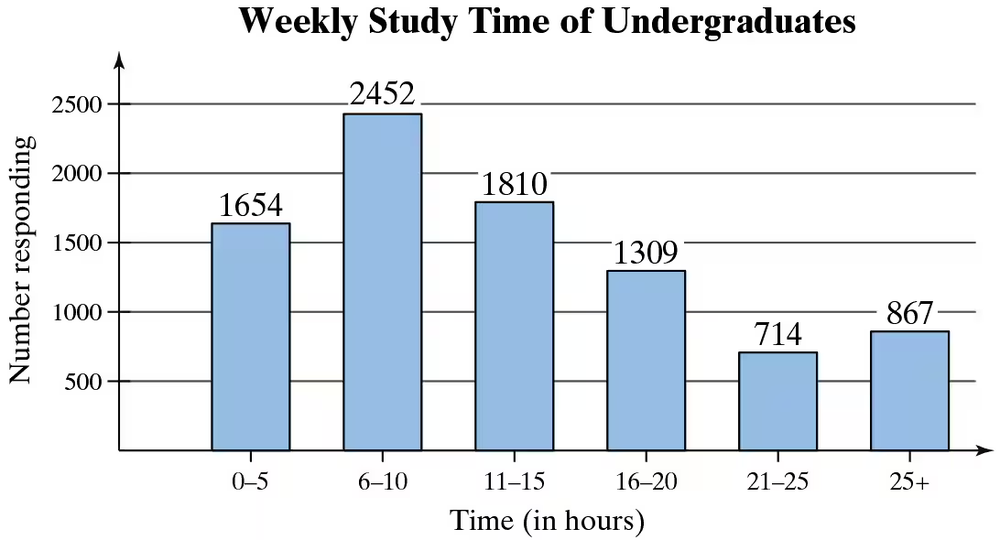
In Exercises 35–38, the bar graph shows the results of a survey in which 8806 undergraduate students were asked how many hours they spend on studying and other academic activities outside of class in a typical week. (Source: American College Health Association)

37. Find the probability of randomly selecting an undergraduate who does not study from 6 to 10 hours per week.

39. You are given that P(A) = 0.15 and P(B) = 0.40. Do you have enough information to find P(A or B)? Explain.

In Exercises 1-4, identify the sample space of the probability experiment and determine the number of outcomes in the event. Draw a tree diagram when appropriate.

3. Experiment: Choosing a month of the year

Event: Choosing a month that begins with the letter J

In Exercises 5 and 6, use the Fundamental Counting Principle.

6. The state of Virginia's license plates have three letters and four digits. Assuming that any letter or digit can be used, how many different license plates are possible?

In Exercises 7-12, classify the statement as an example of classical probability, empirical probability, or subjective probability. Explain your reasoning.

8. The probability of randomly selecting five cards of the same suit from a standard deck of 52 playing cards is about 0.002.

In Exercises 7-12, classify the statement as an example of classical probability, empirical probability, or subjective probability. Explain your reasoning.

11. The probability of rolling 2 six-sided dice and getting a sum of 9 is 1/9.

In Exercises 13 and 14, use the table, which shows the approximate distribution of the sizes of firms for a recent year. (Adapted from North American Industry Classification System)

13. Find the probability that a randomly selected firm will have more than four employees.

Telephone Numbers The telephone numbers for a region of Pennsylvania have an area code of 570. The next seven digits represent the local telephone numbers for that region. These cannot begin with a 0 or 1. In Exercises 15 and 16, assume your cousin lives within the given area code.

16. What is the probability of not randomly generating your cousin's telephone number on the first try?

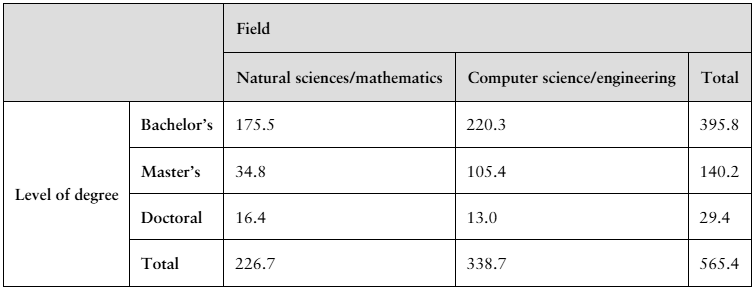
The table shows the numbers (in thousands) of earned degrees by level in two different fields, conferred in the United States in a recent year. (Source: U.S. National Center for Education Statistics)

A person who earned a degree in the year is randomly selected. Find the probability that the degree earned by the person is a

a. bachelor's degree.

The table shows the numbers (in thousands) of earned degrees by level in two different fields, conferred in the United States in a recent year. (Source: U.S. National Center for Education Statistics)

A person who earned a degree in the year is randomly selected. Find the probability that the degree earned by the person is a

g. bachelor's degree and the degree is in natural sciences/mathematics.

The table shows the numbers (in thousands) of earned degrees by level in two different fields, conferred in the United States in a recent year. (Source: U.S. National Center for Education Statistics)

A person who earned a degree in the year is randomly selected. Find the probability that the degree earned by the person is a

g. bachelor's degree and the degree is in natural sciences/mathematics.

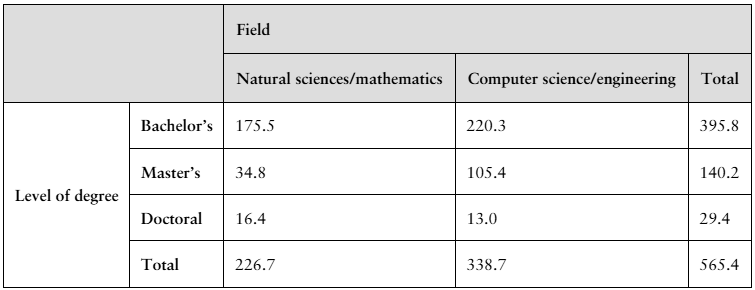
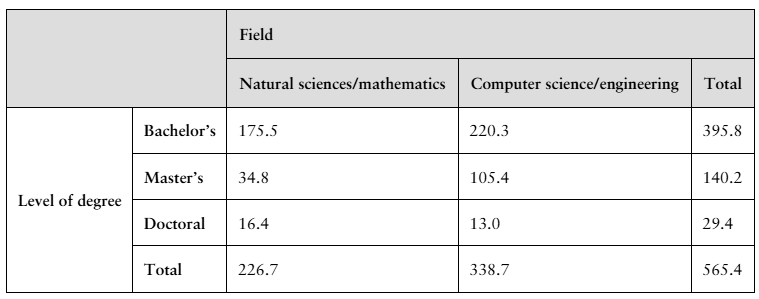
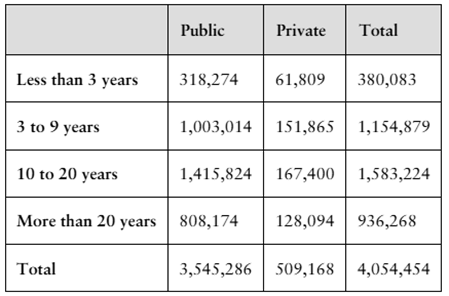
The table shows the results of a survey in which 3,545,286 public and 509,168 private school teachers were asked about their full-time teaching experience.

Are the events “being a public school teacher” and “having more than 20 years of full-time teaching experience” independent? Explain.

4. Determine whether the events are mutually exclusive. Then determine whether the events are independent or dependent. Explain your reasoning.

Event A: A bowler having the highest game in a 40-game tournament

Event B: Losing the bowling tournament

6. A shipment of 250 netbooks contains 3 defective units. Determine how many ways a vending company can buy three of these units and receive

c. at least one good unit.

Your dorm enters 15 out of 65 plastic numbered ducks in a duck race. The ducks are all dumped into a stream and drift to the finish line. What is the probability that three of your dorm's ducks finish first, second, and third?

A person's building access code is their first and last initials and four digits.

You know a person's first name only, and you know that the last digit is odd. What is the probability of guessing this person's code on the first try?

In Exercises 45-48, use combinations and permutations.

46. Five players on a basketball team must each choose one of the five players on the opposing team to defend. In how many ways can the players choose their defensive assignments?

In Exercises 45-48, use combinations and permutations.

48. An employer must hire 2 people from a list of 13 applicants. In how many ways can the employer choose to hire the two people?

In Exercises 49-53, use counting principles to find the probability.

50. A security code consists of three letters and one digit. The first letter cannot be A, B, or C. What is the probability of guessing the security code on the first try?

In Exercises 49-53, use counting principles to find the probability.

51. A shipment of 200 calculators contains 3 defective units. What is the probability that a sample of three calculators will have

c. at least one defective calculator?

In Exercises 49-53, use counting principles to find the probability.

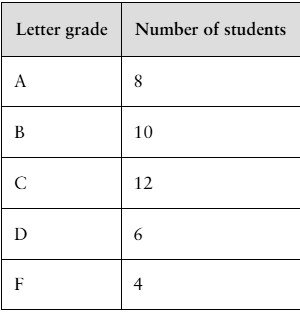
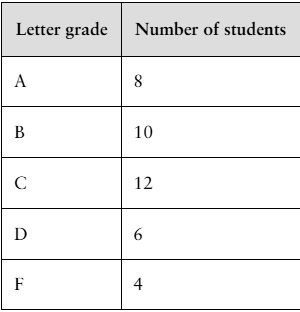
52. A class of 40 students takes a statistics exam. The results are shown in the table at the left. Three students are selected at random. What is the probability that

b. all three students received a C or better?

In Exercises 49-53, use counting principles to find the probability.

52. A class of 40 students takes a statistics exam. The results are shown in the table at the left. Three students are selected at random. What is the probability that

d. all three students received a B or a C?

In Exercises 49-53, use counting principles to find the probability.

53. A corporation has six male senior executives and four female senior executives. Four senior executives are chosen at random to attend a technology seminar. What is the

probability of choosing

c. two men and two women?

In Exercises 49-53, use counting principles to find the probability.

53. A corporation has six male senior executives and four female senior executives. Four senior executives are chosen at random to attend a technology seminar. What is the

probability of choosing

b. four women?

In Exercises 19-22, determine whether the events are independent or dependent. Explain your reasoning.

19. Tossing a coin four times and getting four heads, and then tossing it a fifth time and getting a head

In Exercises 19-22, determine whether the events are independent or dependent. Explain your reasoning.

22. Getting high grades and being awarded an academic scholarship

You work in the security department of a bank’s website. To access their accounts, customers of the bank must create an 8-digit password. It is your job to determine the password requirements for these accounts. Security guidelines state that for the website to be secure, the probability that an 8-digit password is guessed on one try must be less than 1/60^8, assuming all passwords are equally likely.

Your job is to use the probability techniques you have learned in this chapter to decide what requirements a customer must meet when choosing a password, including what sets of characters are allowed, so that the website is secure according to the security guidelines.

2. Answering the Question

a. What password requirements would you set? What characters would be allowed?

You work in the security department of a bank’s website. To access their accounts, customers of the bank must create an 8-digit password. It is your job to determine the password requirements for these accounts. Security guidelines state that for the website to be secure, the probability that an 8-digit password is guessed on one try must be less than 1/60^8, assuming all passwords are equally likely.

Your job is to use the probability techniques you have learned in this chapter to decide what requirements a customer must meet when choosing a password, including what sets of characters are allowed, so that the website is secure according to the security guidelines.

3. For additional security, each customer creates a 5-digit PIN (personal identification number). The table on the right shows the 10 most commonly chosen 5-digit PINs. From the table, you can see that more than a third of all 5-digit PINs could be guessed by trying these 10 numbers. To discourage customers from using predictable PINs, you consider prohibiting PINs that use the same digit more than once.

b. Would you decide to prohibit PINs that use the same digit more than once? Explain.

2. How many possible variations are there in Mozart's Musical Dice Game minuet? Explain.

5. Use technology to randomly select two numbers from 1 to 6. Find the sum and subtract 1 to obtain a total.

a. What is the theoretical probability of each total from 1 to 11?

b. Use this procedure to select 100 totals from 1 to 11. Tally your results and compare them with the probabilities in part (a).