Back
BackProblem 3.RE.42
In Exercises 41-44, perform the indicated calculation.
42. 8P6
Problem 3.RE.44
In Exercises 41-44, perform the indicated calculation.
44. (5C3)/(10C3)
Problem 3.T.4a
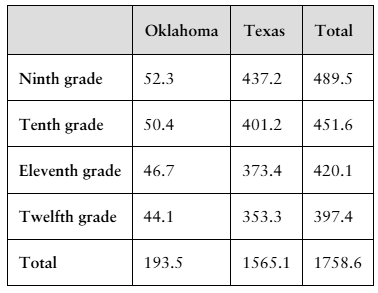
4. The table on the left shows the secondary school student enrollment levels (in thousands by grade) in Oklahoma and Texas schools in a recent year. (Source: U.S. Nation
for Education Statistics)
A student in one of the indicated grades and states is randomly selected. Find the probability of selecting a student who
a. is in ninth grade.
Problem 3.T.4d
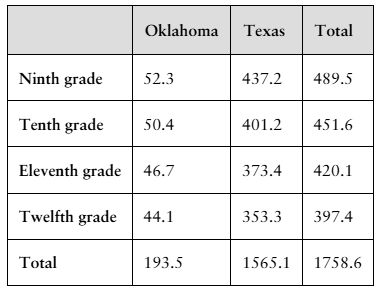
4. The table on the left shows the secondary school student enrollment levels (in thousands by grade) in Oklahoma and Texas schools in a recent year. (Source: U.S. Nation
for Education Statistics)
A student in one of the indicated grades and states is randomly selected. Find the probability of selecting a student who
d. is enrolled in Texas, given that the student is in twelfth grade.
Problem 3.Test.5
5. Which event(s) in Exercise 4 can be considered unusual? Explain your reasoning.
Problem 3.T.7b
7. There are 16 students giving final presentations in your history course.
b. Presentation subjects are based on the units of the course. Unit B is covered by three students, Unit C is covered by five students, and Units A and D are each covered by four students. How many presentation orders are possible when presentations on
the same unit are indistinguishable from each other?
Problem 3.R.1
"In Exercises 1-4, identify the sample space of the probability experiment and determine the number of outcomes in the event. Draw a tree diagram when appropriate.
1. Experiment: Tossing four coins
Event: Getting three heads"
Problem 3.R.4
"In Exercises 1-4, identify the sample space of the probability experiment and determine the number of outcomes in the event. Draw a tree diagram when appropriate.
4. Experiment: Guessing the gender(s) of the three children in a family
Event: Guessing that the family has two boys"
Problem 3.R.5
"In Exercises 5 and 6, use the Fundamental Counting Principle.
5. A student must choose from seven classes to take at 8:00 A.M., four classes to take at 9:00 A.M., and three classes to take at 10:00 A.M. How many ways can the student arrange the schedule?"
Problem 3.RE.20
"In Exercises 19-22, determine whether the events are independent or dependent. Explain your reasoning.
20. Selecting an ace from a standard deck of 52 playing cards, and then selecting a jack from the deck without replacing the ace"
Problem 3.RE.21
"In Exercises 19-22, determine whether the events are independent or dependent. Explain your reasoning.
21. Taking a driver's education course and passing the driver's license exam"
Problem 3.R.17
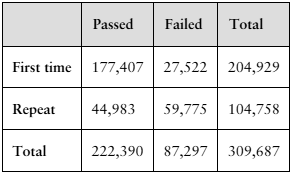
In Exercises 17 and 18, use the table, which shows the numbers of first-time and repeat U.S. nursing students taking the National Council Licensure Examination (NCLEX-RN® exam) to pass or fail in a recent year. (Adapted from National Council Licensure Examinations)
17. Find the probability that a student took the exam for the first time, given that the student failed.
Problem 3.R.18
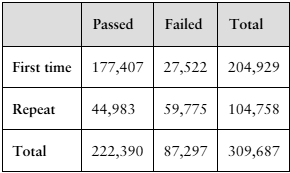
"In Exercises 17 and 18, use the table, which shows the numbers of first-time and repeat U.S. nursing students taking the National Council Licensure Examination (NCLEX-RN® exam) to pass or fail in a recent year. (Adapted from National Council Licensure Examinations)
18. Find the probability that a student passed, given that the student repeated the exam."
Problem 3.1.2a
2. Determine whether each number could represent the probability of an event. Explain your reasoning. a. 25/25
Problem 3.1.2b
2. Determine whether each number could represent the probability of an event. Explain your reasoning. b. 333.3%
Problem 3.1.2c
2. Determine whether each number could represent the probability of an event. Explain your reasoning. c. 2.3
Problem 3.1.2d
2. Determine whether each number could represent the probability of an event. Explain your reasoning. d. -0.0004
Problem 3.1.3
3. Explain why the statement is incorrect: The probability of rain is 150%.
Problem 3.1.9
True or False? In Exercises 7-10, determine whether the statement is true or false. If it is false, rewrite it as a true statement.
9. A probability of 1/10 indicates an unusual event.
Problem 3.1.11
Matching Probabilities In Exercises 11-16, match the event with its probability.
a. 0.95
b. 0.005
c. 0.25
d. 0
e. 0.375
f. 0.5
11. A random number generator is used to select a number from 1 to 100. What is the probability of selecting the number 153?
Problem 3.1.14
Matching Probabilities In Exercises 11-16, match the event with its probability.
a. 0.95
b. 0.005
c. 0.25
d. 0
e. 0.375
f. 0.5
14. A game show contestant must randomly select a door. One door doubles her money while the other three doors leave her with no winnings. What is the probability she selects the
door that doubles her money?
Problem 3.1.16
Matching Probabilities In Exercises 11-16, match the event with its probability.
a. 0.95
b. 0.005
c. 0.25
d. 0
e. 0.375
f. 0.5
16. You toss a coin four times. What is the probability of tossing tails exactly half of the time?
Problem 3.1.19
Finding the Probability of the Complement of an Event In Exercises 17-20, the probability that an event will happen is given. Find the probability that the event will not happen.
19. P(E)=0.03
Problem 3.1.21
Finding the Probability of an Event In Exercises 21-24, the probability that an event will not happen is given. Find the probability that the event will happen.
21. P(E') =0.95
Problem 3.1.23
Finding the Probability of an Event In Exercises 21-24, the probability that an event will not happen is given. Find the probability that the event will happen.
23. P(E')=3/4
Problem 3.1.25
Identifying the Sample Space of a Probability Experiment In Exercises 25-32, identify the sample space of the probability experiment and determine the number of outcomes in the sample space. Draw a tree diagram when appropriate.
25. Guessing the initial of a student's middle name
Problem 3.1.28
Identifying the Sample Space of a Probability Experiment In Exercises 25-32, identify the sample space of the probability experiment and determine the number of outcomes in the sample space. Draw a tree diagram when appropriate.
28. Identifying a person's eye color (brown, blue, green, hazel, gray, other) and hair color (black, brown, blonde, red, other).
Problem 3.1.31
Identifying the Sample Space of a Probability Experiment In Exercises 25-32, identify the sample space of the probability experiment and determine the number of outcomes in the sample space. Draw a tree diagram when appropriate.
31. Rolling a pair of six-sided dice
Problem 3.1.34
Identifying Simple Events In Exercises 33-36, determine the number of outcomes in the event. Then decide whether the event is a simple event or not. Explain your reasoning.
34. A spreadsheet is used to randomly generate a number from 1 to 4000. Event B is generating a number less than 500.
Problem 3.1.37
Using the Fundamental Counting Principle In Exercises 37-40, use the Fundamental Counting Principle.
37. Menu A restaurant offers a $15 dinner special that lets you choose from 6 appetizers, 12 entrées, and 8 desserts. How many different meals are available when you select an appetizer, an entrée, and a dessert?