80. Unusual Events Can any of the events in Exercises 75-78 be considered unusual? Explain.
Table of contents
- 1. Intro to Stats and Collecting Data1h 14m
- 2. Describing Data with Tables and Graphs1h 55m
- 3. Describing Data Numerically2h 5m
- 4. Probability2h 16m
- 5. Binomial Distribution & Discrete Random Variables3h 6m
- 6. Normal Distribution and Continuous Random Variables2h 11m
- 7. Sampling Distributions & Confidence Intervals: Mean3h 23m
- Sampling Distribution of the Sample Mean and Central Limit Theorem19m
- Distribution of Sample Mean - Excel23m
- Introduction to Confidence Intervals15m
- Confidence Intervals for Population Mean1h 18m
- Determining the Minimum Sample Size Required12m
- Finding Probabilities and T Critical Values - Excel28m
- Confidence Intervals for Population Means - Excel25m
- 8. Sampling Distributions & Confidence Intervals: Proportion1h 25m
- 9. Hypothesis Testing for One Sample3h 29m
- 10. Hypothesis Testing for Two Samples4h 50m
- Two Proportions1h 13m
- Two Proportions Hypothesis Test - Excel28m
- Two Means - Unknown, Unequal Variance1h 3m
- Two Means - Unknown Variances Hypothesis Test - Excel12m
- Two Means - Unknown, Equal Variance15m
- Two Means - Unknown, Equal Variances Hypothesis Test - Excel9m
- Two Means - Known Variance12m
- Two Means - Sigma Known Hypothesis Test - Excel21m
- Two Means - Matched Pairs (Dependent Samples)42m
- Matched Pairs Hypothesis Test - Excel12m
- 11. Correlation1h 6m
- 12. Regression1h 50m
- 13. Chi-Square Tests & Goodness of Fit1h 57m
- 14. ANOVA1h 57m
4. Probability
Basic Concepts of Probability
Problem 3.RE.3
Textbook Question
In Exercises 1-4, identify the sample space of the probability experiment and determine the number of outcomes in the event. Draw a tree diagram when appropriate.
3. Experiment: Choosing a month of the year
Event: Choosing a month that begins with the letter J
 Verified step by step guidance
Verified step by step guidance1
Step 1: Understand the problem. The probability experiment involves choosing a month of the year, and the event is choosing a month that begins with the letter 'J'. There are 12 months in a year, and we need to identify which of these months meet the criteria of starting with 'J'.
Step 2: Identify the sample space. The sample space is the set of all possible outcomes of the experiment, which includes all 12 months: {January, February, March, April, May, June, July, August, September, October, November, December}.
Step 3: Determine the subset of the sample space that satisfies the event condition. The months that begin with the letter 'J' are {January, June, July}.
Step 4: Count the number of outcomes in the event. The subset {January, June, July} contains 3 outcomes, so the number of outcomes in the event is 3.
Step 5: Draw a tree diagram if needed. A tree diagram can visually represent the choices. Start with a single branch for the experiment (choosing a month), then create branches for each month, and highlight the branches corresponding to January, June, and July to show the event.
 Verified video answer for a similar problem:
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
3mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Sample Space
The sample space of a probability experiment is the set of all possible outcomes. In the context of choosing a month of the year, the sample space consists of the twelve months: January, February, March, April, May, June, July, August, September, October, November, and December. Understanding the sample space is crucial for calculating probabilities and determining the likelihood of specific events.
Recommended video:
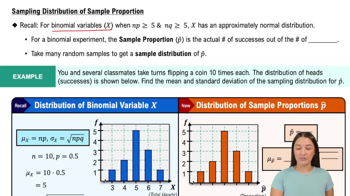
Sampling Distribution of Sample Proportion
Event
An event is a specific outcome or a set of outcomes from the sample space that we are interested in. In this case, the event is choosing a month that begins with the letter 'J', which includes January and June. Identifying the event helps in calculating the probability of its occurrence based on the sample space.
Recommended video:

Probability of Multiple Independent Events
Tree Diagram
A tree diagram is a visual representation used to illustrate all possible outcomes of a probability experiment. It branches out from a starting point, showing each possible outcome at each stage. In this scenario, while a tree diagram may not be necessary for a single selection of a month, it can be useful for more complex experiments involving multiple choices or events.
Recommended video:
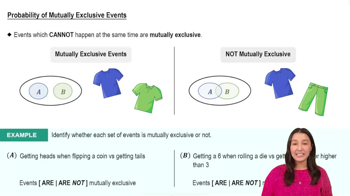
Probability of Mutually Exclusive Events

 5:37m
5:37mWatch next
Master Introduction to Probability with a bite sized video explanation from Patrick
Start learningRelated Videos
Related Practice
Textbook Question
