Back
BackProblem 3.2.28a
"Using the Multiplication Rule In Exercises 19-32, use the Multiplication Rule.
28. Blood Types The probability that a Latinx American person in the United States has type A+ blood is 29%. Four Latinx American people in the United States are selected at random. (Source: American National Red Cross)
a. Find the probability that all four have type A+ blood."
Problem 3.2.36
"According to Bayes’ Theorem, the probability of event A , given that event B has occurred, is
P(A|B) = P(A) * P(B|A)P(A) * P(B|A) + P(A') * P(B|A').
In Exercises 33–38, use Bayes’ Theorem to find P(A|B).
36. P(A) = 0.62, P(A') = 0.38, P(B|A) = 0.41 , and P(B|A') = 0.17 "
Problem 3.2.21a
"Using the Multiplication Rule In Exercises 19-32, use the Multiplication Rule.
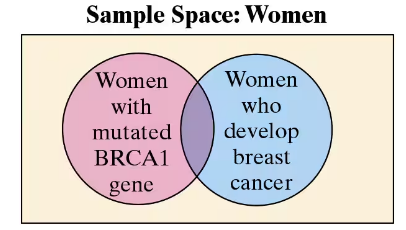
21. BRCA1 Gene Research has shown that approximately 1 woman in 400 carries a mutation of the BRCA1 gene. About 64% of women with this mutation develop breast
cancer. Find the probability that a randomly selected woman will carry the mutation of the BRCA1 gene and will develop breast cancer. (Source: National Cancer Institute)
Problem 3.2.22
"Using the Multiplication Rule In Exercises 19-32, use the Multiplication Rule.
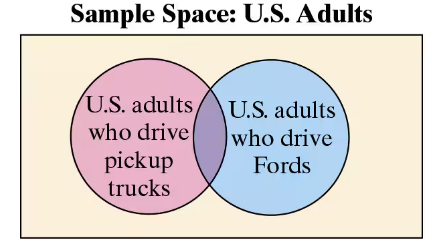
22.Pickup Trucks In a survey, 510 U.S. adults were asked whether they drive a pickup truck and whether they drive a Ford. The results showed that three in twenty adults surveyed drive a Ford. Of the adults surveyed that drive Fords, nine in twenty drive a pickup truck. Find the probability that a randomly selected adult drives a Ford and drives a pickup truck.
Problem 3.2.1a
"1. What is the difference between independent and dependent events?
Problem 3.2.2
"2. Give an example of
a. two events that are independent.
b. two events that are dependent."
Problem 3.2.5
"True or False? In Exercises 5 and 6, determine whether the statement is true or false. If it is false, rewrite it as a true statement.
5. If two events are independent, then P(A|B) = P(B)."
Problem 3.2.9
"Classifying Events as Independent or Dependent In Exercises 9-14, determine whether the events are independent or dependent. Explain your reasoning.
9. Selecting a king from a standard deck of 52 playing cards, replacing it, and then selecting a queen from the deck"
Problem 3.2.10
"Classifying Events as Independent or Dependent In Exercises 9-14, determine whether the events are independent or dependent. Explain your reasoning.
10. A father having hazel eyes and a daughter having hazel eyes"
Problem 3.2.12
"Classifying Events as Independent or Dependent In Exercises 9-14, determine whether the events are independent or dependent. Explain your reasoning.
12. Not putting money in a parking meter and getting a parking ticket"
Problem 3.2.13
"Classifying Events as Independent or Dependent In Exercises 9-14, determine whether the events are independent or dependent. Explain your reasoning.
13. Rolling a six-sided die and then rolling the die a second time so that the sum of the two rolls is five"
Problem 3.2.15
"Classifying Events Based on Studies In Exercises 15-18, identify the two events described in the study. Do the results indicate that the events are independent or dependent? Explain your reasoning.
15. A study was conducted to debunk the idea that abilities in music and math are related. Instead, the study showed a strong relationship between achievements in music and math.
(Source: University of Kansas)"
Problem 3.2.16
"Classifying Events Based on Studies In Exercises 15-18, identify the two events described in the study. Do the results indicate that the events are independent or dependent? Explain your reasoning.
16. A study found no significant association between the use of talc powder and the incidence of ovarian cancer in women. (Source: JAMA)"
Problem 3.3.1
1. When two events are mutually exclusive, why is P(A and B) = 0?
Problem 3.3.4
True or False? In Exercises 3-6, determine whether the statement is true or false. If it is false,
explain why.
4. When two events are independent, they are also mutually exclusive.
Problem 3.3.7
Graphical Analysis In Exercises 7 and 8, determine whether the events shown in the Venn diagram are mutually exclusive. Explain your reasoning.
Problem 3.3.10
Recognizing Mutually Exclusive Events In Exercises 9–12, determine whether the events are mutually exclusive. Explain your reasoning.
10. Event A: Randomly select a student with a birthday in April.
Event B: Randomly select a student with a birthday in May.
Problem 3.3.13
13. Students A physics class has 40 students. Of these, 12 students are physics majors and 16 students are minoring in math. Of the physics majors, three are minoring in math. Find the probability that a randomly selected student is minoring in math or a physics major.
Problem 3.3.16
16. Can Defects Of the cans produced by a company, 96% do not have a puncture, 93% do not have a smashed edge, and 89.3% have neither a puncture nor a smashed edge. Find
the probability that a randomly selected can does not have a puncture or a smashed edge.
Problem 3.3.17c
17. Selecting a Card A card is selected at random from a standard deck of 52 playing cards. Find the probability of each event.
c. Randomly selecting a 9 or a face card
Problem 3.3.18b
18. Rolling a Die You roll a die. Find the probability of each event.
b. Rolling a 2 or an odd number
Problem 3.3.24c
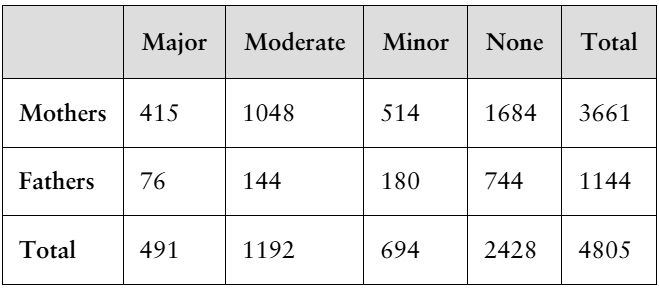
Mental Health A survey asks 4805 parents the severity of the mental issues they experienced from the coronavirus pandemic. The results are shown in the table. A parent is randomly selected from the sample. Find the probability of each event. (Adapted from Kaiser Family Foundation)
c. The parent did not have major mental health issues or is a mother.
Problem 3.3.25b
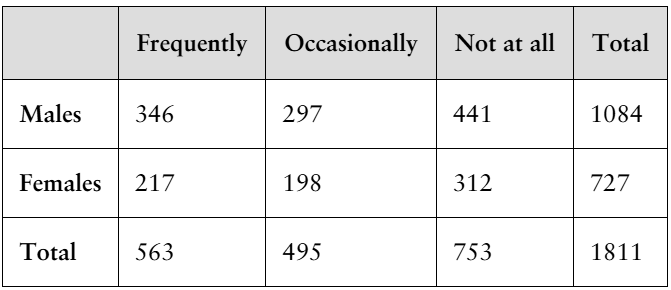
25. Working from Home The table shows the results of a survey that asked 1811 people how often they work from home. A person is selected at random from the sample. Find the probability of each event.
b. The person is female or does not work from home.
Problem 3.3.26a
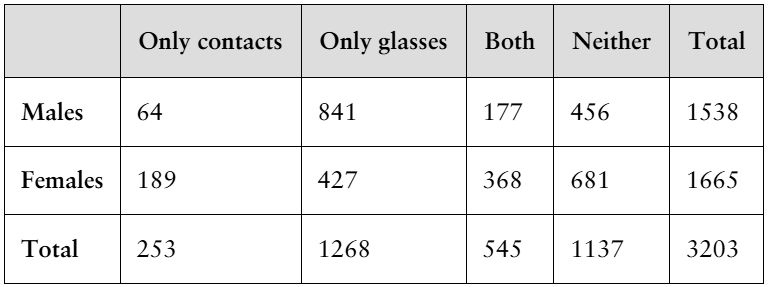
26. Eye Survey The table shows the results of a survey that asked 3203 people whether they wore contacts or glasses. A person is selected at random from the sample. Find the probability of each event.
a. The person wears only contacts or only glasses.
Problem 3.3.26d
26. Eye Survey The table shows the results of a survey that asked 3203 people whether they wore contacts or glasses. A person is selected at random from the sample. Find the probability of each event.
d. The person is male or does not wear glasses.
Problem 3.3.29
29. Explain, in your own words, why in the Addition Rule for P(A or B or C), P(A and B and C) is added at the end of the formula.
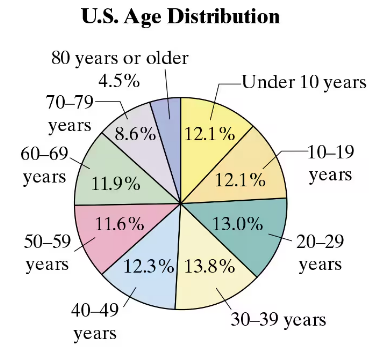
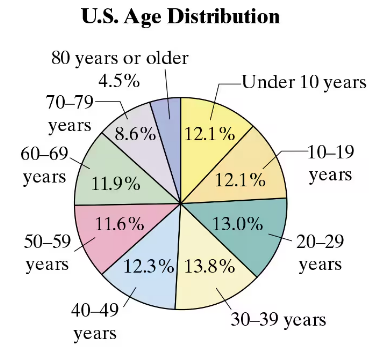
Problem 3.3.19a
U.S. Age Distribution The projected percent distribution of the U.S. population for 2025 is shown in the pie chart. Find the probability of each event. (Source: U.S. Census
Bureau)
a. Randomly selecting someone who is under 10 years old
Problem 3.3.19c
19. U.S. Age Distribution The projected percent distribution of the U.S. population for 2025 is shown in the pie chart. Find the probability of each event. (Source: U.S. Census
Bureau)
c. Randomly selecting someone who is not 60 years or over
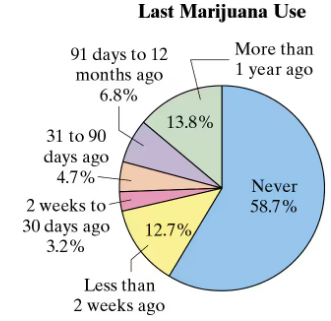
Problem 3.3.20a
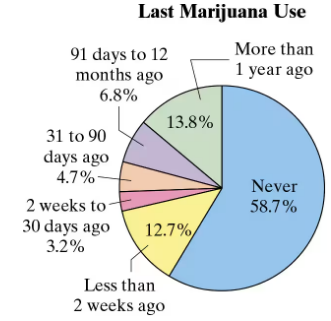
Marijuana Use The percent distribution of the last marijuana use (either medical or nonmedical) for a sample of 13,373 college students is shown in the pie chart. Find the
probability of each event. (Source: American College Health Association)
a. Randomly selecting a student who never used marijuana
Problem 3.3.20d
Marijuana Use The percent distribution of the last marijuana use (either medical or nonmedical) for a sample of 13,373 college students is shown in the pie chart. Find the
probability of each event. (Source: American College Health Association)
d. Randomly selecting a student who has not used marijuana within the last 12 months