Here are the essential concepts you must grasp in order to answer the question correctly.
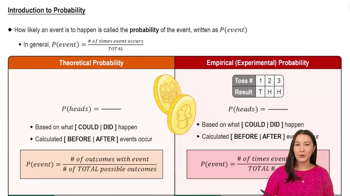
Probability
Probability is a measure of the likelihood that an event will occur, expressed as a number between 0 and 1. An event with a probability of 0 means it cannot happen, while a probability of 1 means it is certain to happen. In the context of rolling a die, the probability of an event can be calculated by dividing the number of favorable outcomes by the total number of possible outcomes.
Recommended video:
Introduction to Probability
Sample Space
The sample space is the set of all possible outcomes of a random experiment. For a single roll of a fair six-sided die, the sample space consists of the numbers {1, 2, 3, 4, 5, 6}. Understanding the sample space is crucial for calculating probabilities, as it provides the basis for determining how many outcomes are favorable for a given event.
Recommended video:
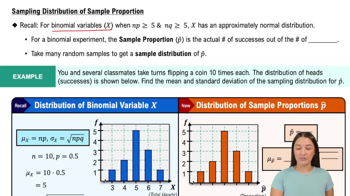
Sampling Distribution of Sample Proportion
Compound Events
A compound event is an event that consists of two or more simple events. In this case, rolling a 2 or an odd number involves two simple events: rolling a 2 and rolling an odd number (1, 3, or 5). To find the probability of a compound event, one must consider the individual probabilities of each simple event and account for any overlap, ensuring that outcomes are not double-counted.
Recommended video:
Probability of Multiple Independent Events