Mental Health A survey asks 4805 parents the severity of the m...

Question

Mental Health A survey asks 4805 parents the severity of the mental issues they experienced from the coronavirus pandemic. The results are shown in the table. A parent is randomly selected from the sample. Find the probability of each event. (Adapted from Kaiser Family Foundation)

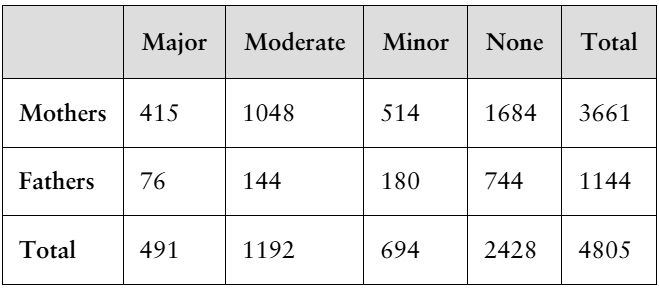
c. The parent did not have major mental health issues or is a mother.

<IMAGE>

c. The parent did not have major mental health issues or is a mother.

Accepted Answer

Hi, everyone, let's take a look at this practice problem. This problem says a company surveyed 4300 employees about their experience with remote work. The results are shown in the table. If an employee is randomly selected from the sample, what is the probability that they either did not report high job satisfaction or from the IT department? Below text we're given a table that has 5 columns and 4 rows. The columns correspond to the satisfaction rating, and we have high, medium, low, none, and the final column for total. And the rows are labeled with the department, so we have IT, HR sales, and then a final row for totals. Now for the first row for the IT, we have 320 employees that reported high satisfaction, 700 for medium, 380 for low, 900 for none, or a total of 2300. The next row is for the HR department, and it has 80 employees for high satisfaction. 250 for medium, 180 for low, 490 for none, for a total of 1000. The next row is for sales, and it had 60 employees with high satisfaction, 200 with medium, 240 with low, 500 for none. And a total of 1000. And the final row is for totals, so this will be the total of each of our satisfaction ratings. And so we had 460 for high. 1150 for medium, 800 for low, 1890 for none, or a total of 4300. And we're also given four possible choices as our answers. For choice A, we have 0.033. For choice B, we have 0.967. For choice C, we have 0.460, and for choice D, we have 0.540. Now, the first thing we want to do is to define our events. So, for event A, we're gonna say that that are the that's going to be the people that did not report high job satisfaction. And then for event B, We're going to have Those who are in the IT department. So, we want to do now is to figure out how many employees are in both of these events. So we'll start off by determining the number of people that reported not having high job satisfaction. So, we'll call that in of A. And this is just going to be equal to the total number of employees, which, if we read that off of the table, is going to be 4300. Minus those that reported by job satisfaction, which again, if we read that off at our table, is going to be 460. And so that means that the number of people that correspond to event A is going to be equal to. 3840. Next, we'll need to find the number of people that are in our IT departments. So that's going to be in of B. And here we can just read this directly off of our table, since the total number of people in the IT department is going to be 2300. Now, we need to figure out the number of people that are in the IT department and did not report high job satisfaction. So we're gonna call that in of a intersect B. And so this is just going to be equal to the number of people in our IT department, which is 2300. Minus the number of people that reported high satisfaction and being in the IT department. And so that is from our table, 320. And evaluating this, this is going to be equal to 1980. So now we can actually figure out our probabilities. So we're actually looking for the probability P. Of a union be. And so, this is going to be equal to. The number of people that did not report high job satisfaction, that's gonna be end of A. Plus, the number of people in the IT department, which is going to be in of B. But we do not want to overcount. And so we need to subtract off. The people that are both in the IT department and did not report I job satisfaction. So it'll be minus N of A intersect B. And this whole quantity is going to be divided by. Our number, total number of employees, so it'll be in of total. And so this is going to be equal to for N of A, we have 3840, then we'll have plus N of B, which is 2300. Minus of a intersect B, which is 1980, and that whole quantity is going to be divided by the total number of employees, which is 4300. And so when we evaluate this expression, this is going to be approximately equal to. 0.967. So here we just round it to three decimal places. So this is the answer that we were looking for for this problem. And if we look at our answer choices, this actually corresponds to answer choice B. So I hope that this explanation has been useful, and I'll see you in the next video.

Key Concepts

Probability

Complementary Events

Conditional Probability

Watch next