Cola Weights Data Set 37 “Cola Weights and Volumes” in Appendix B lists the weights (lb) of the contents of cans of cola from four different samples: (1) regular Coke, (2) Diet Coke, (3) regular Pepsi, and (4) Diet Pepsi. The results from analysis of variance are shown in the Minitab display below. What is the null hypothesis for this analysis of variance test? Based on the displayed results, what should you conclude about H_knot. What do you conclude about equality of the mean weights from the four samples?
Table of contents
- 1. Intro to Stats and Collecting Data1h 14m
- 2. Describing Data with Tables and Graphs1h 55m
- 3. Describing Data Numerically2h 5m
- 4. Probability2h 16m
- 5. Binomial Distribution & Discrete Random Variables3h 6m
- 6. Normal Distribution and Continuous Random Variables2h 11m
- 7. Sampling Distributions & Confidence Intervals: Mean3h 23m
- Sampling Distribution of the Sample Mean and Central Limit Theorem19m
- Distribution of Sample Mean - Excel23m
- Introduction to Confidence Intervals15m
- Confidence Intervals for Population Mean1h 18m
- Determining the Minimum Sample Size Required12m
- Finding Probabilities and T Critical Values - Excel28m
- Confidence Intervals for Population Means - Excel25m
- 8. Sampling Distributions & Confidence Intervals: Proportion1h 12m
- 9. Hypothesis Testing for One Sample3h 29m
- 10. Hypothesis Testing for Two Samples4h 50m
- Two Proportions1h 13m
- Two Proportions Hypothesis Test - Excel28m
- Two Means - Unknown, Unequal Variance1h 3m
- Two Means - Unknown Variances Hypothesis Test - Excel12m
- Two Means - Unknown, Equal Variance15m
- Two Means - Unknown, Equal Variances Hypothesis Test - Excel9m
- Two Means - Known Variance12m
- Two Means - Sigma Known Hypothesis Test - Excel21m
- Two Means - Matched Pairs (Dependent Samples)42m
- Matched Pairs Hypothesis Test - Excel12m
- 11. Correlation1h 6m
- 12. Regression1h 50m
- 13. Chi-Square Tests & Goodness of Fit1h 57m
- 14. ANOVA1h 57m
9. Hypothesis Testing for One Sample
Steps in Hypothesis Testing
Problem 13.2.11
Textbook Question
In Exercises 9–12, use the sign test for the claim involving nominal data.
Overtime Rule in Football Before the overtime rule in the National Football League was changed in 2011, among 460 overtime games, 252 were won by the team that won the coin toss at the beginning of overtime. Using a 0.05 significance level, test the claim that the coin toss is fair in the sense that neither team has an advantage by winning it. Does the coin toss appear to be fair?
 Verified step by step guidance
Verified step by step guidance1
Identify the null and alternative hypotheses. The null hypothesis (H₀) is that the coin toss is fair, meaning the probability of winning after winning the coin toss is 0.5. The alternative hypothesis (H₁) is that the coin toss is not fair, meaning the probability of winning after winning the coin toss is not 0.5.
Determine the test statistic for the sign test. In this case, the number of successes (games won by the team that won the coin toss) is 252, and the total number of trials (overtime games) is 460. Under the null hypothesis, the expected number of successes is 460 × 0.5 = 230.
Calculate the test statistic. The test statistic for the sign test is based on the binomial distribution. Use the formula for the z-score: z = (x - np) / sqrt(np(1-p)), where x is the observed number of successes, n is the total number of trials, and p is the probability under the null hypothesis (0.5).
Determine the critical value or p-value. Since the significance level is 0.05, use a two-tailed test to find the critical z-values or calculate the p-value corresponding to the observed z-score. Compare the p-value to the significance level to decide whether to reject the null hypothesis.
Make a conclusion. If the p-value is less than 0.05 or the test statistic falls outside the critical region, reject the null hypothesis and conclude that the coin toss is not fair. Otherwise, fail to reject the null hypothesis and conclude that there is not enough evidence to suggest the coin toss is unfair.
 Verified video answer for a similar problem:
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
3mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Sign Test
The sign test is a non-parametric statistical method used to evaluate the median of a single sample or to compare two related samples. It is particularly useful for nominal data, where the outcomes can be categorized but not ranked. In this context, it helps determine if there is a significant difference in the outcomes of games won by the team that won the coin toss versus those that did not.
Recommended video:
Guided course
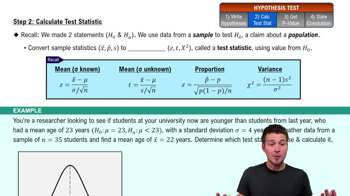
Step 2: Calculate Test Statistic
Null Hypothesis and Significance Level
In hypothesis testing, the null hypothesis represents a statement of no effect or no difference, which researchers aim to test against. The significance level, often denoted as alpha (α), is the threshold for determining whether to reject the null hypothesis. In this case, a significance level of 0.05 indicates that there is a 5% risk of concluding that a difference exists when there is none.
Recommended video:
Guided course

Step 1: Write Hypotheses
Nominal Data
Nominal data is a type of categorical data that represents distinct categories without any inherent order or ranking. Examples include gender, race, or, in this case, the outcome of a coin toss (win or lose). Understanding nominal data is crucial for applying the sign test, as it focuses on the frequency of occurrences within these categories rather than their numerical values.
Recommended video:
Guided course
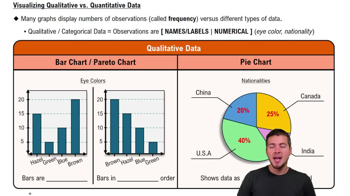
Visualizing Qualitative vs. Quantitative Data

 6:21m
6:21mWatch next
Master Step 1: Write Hypotheses with a bite sized video explanation from Patrick
Start learningRelated Videos
Related Practice
Textbook Question
