Accuracy of Fingerprint Identifications An experiment was conducted to compare the accuracy of fingerprint experts to the accuracy of novices (based on data from “Identifying Fingerprint Expertise,” by Tangen, Thompson, and McCarthy, Psychological Science, Vol. 22, No. 8). The data in the table are based on trials in which the evaluators were given matching fingerprints. Use a 0.05 significance level to determine whether correct identification is independent of whether the evaluator is an expert or a novice.
Table of contents
- 1. Intro to Stats and Collecting Data1h 14m
- 2. Describing Data with Tables and Graphs1h 55m
- 3. Describing Data Numerically2h 5m
- 4. Probability2h 16m
- 5. Binomial Distribution & Discrete Random Variables3h 6m
- 6. Normal Distribution and Continuous Random Variables2h 11m
- 7. Sampling Distributions & Confidence Intervals: Mean3h 23m
- Sampling Distribution of the Sample Mean and Central Limit Theorem19m
- Distribution of Sample Mean - Excel23m
- Introduction to Confidence Intervals15m
- Confidence Intervals for Population Mean1h 18m
- Determining the Minimum Sample Size Required12m
- Finding Probabilities and T Critical Values - Excel28m
- Confidence Intervals for Population Means - Excel25m
- 8. Sampling Distributions & Confidence Intervals: Proportion1h 12m
- 9. Hypothesis Testing for One Sample3h 29m
- 10. Hypothesis Testing for Two Samples4h 50m
- Two Proportions1h 13m
- Two Proportions Hypothesis Test - Excel28m
- Two Means - Unknown, Unequal Variance1h 3m
- Two Means - Unknown Variances Hypothesis Test - Excel12m
- Two Means - Unknown, Equal Variance15m
- Two Means - Unknown, Equal Variances Hypothesis Test - Excel9m
- Two Means - Known Variance12m
- Two Means - Sigma Known Hypothesis Test - Excel21m
- Two Means - Matched Pairs (Dependent Samples)42m
- Matched Pairs Hypothesis Test - Excel12m
- 11. Correlation1h 6m
- 12. Regression1h 50m
- 13. Chi-Square Tests & Goodness of Fit1h 57m
- 14. ANOVA1h 57m
9. Hypothesis Testing for One Sample
Steps in Hypothesis Testing
Problem 9.4.4
Textbook Question
Robust What does it mean when we say that the F test described in this section is not robust against departures from normality?
 Verified step by step guidance
Verified step by step guidance1
Understand the term 'robust': In statistics, a test is considered robust if it remains valid and reliable even when its assumptions are violated to some extent. For the F-test, one key assumption is that the data in each group being compared comes from a normal distribution.
Identify the assumption of normality: The F-test assumes that the populations being compared are normally distributed. This means that the shape of the data distribution in each group should resemble a bell curve.
Explain the impact of non-robustness: When we say the F-test is 'not robust against departures from normality,' it means that if the data significantly deviates from a normal distribution (e.g., it is skewed or has heavy tails), the results of the F-test may no longer be accurate or reliable.
Discuss potential consequences: If the assumption of normality is violated, the F-test may produce incorrect p-values, leading to an increased risk of Type I errors (rejecting a true null hypothesis) or Type II errors (failing to reject a false null hypothesis).
Suggest alternatives: In cases where normality is violated, consider using non-parametric tests (e.g., the Kruskal-Wallis test) or transforming the data to better meet the normality assumption before applying the F-test.
 Verified video answer for a similar problem:
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
1mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
F Test
The F test is a statistical method used to compare variances between two or more groups. It helps determine if the group means are significantly different from each other, based on the ratio of variances. The test assumes that the data follows a normal distribution and is commonly used in ANOVA (Analysis of Variance) to assess the impact of one or more factors.
Recommended video:
Guided course
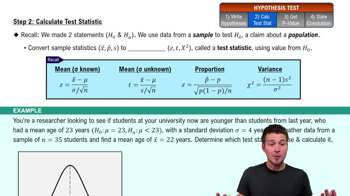
Step 2: Calculate Test Statistic
Normality Assumption
The normality assumption refers to the requirement that the data being analyzed should follow a normal distribution for certain statistical tests, including the F test. When this assumption is violated, the results of the test may become unreliable, leading to incorrect conclusions about the significance of the differences between groups.
Recommended video:
Guided course

Finding Standard Normal Probabilities using z-Table
Robustness in Statistics
Robustness in statistics refers to the ability of a statistical test to remain valid under violations of its assumptions. A test is considered robust if it can still provide reliable results even when the data deviates from the ideal conditions, such as normality. The F test is described as not robust against departures from normality, meaning that its results can be significantly affected when the data does not follow a normal distribution.
Recommended video:
Guided course

Parameters vs. Statistics

 6:21m
6:21mWatch next
Master Step 1: Write Hypotheses with a bite sized video explanation from Patrick
Start learningRelated Videos
Related Practice
Textbook Question
