Clinical Trial of Echinacea In a clinical trial of the effecti...

Question

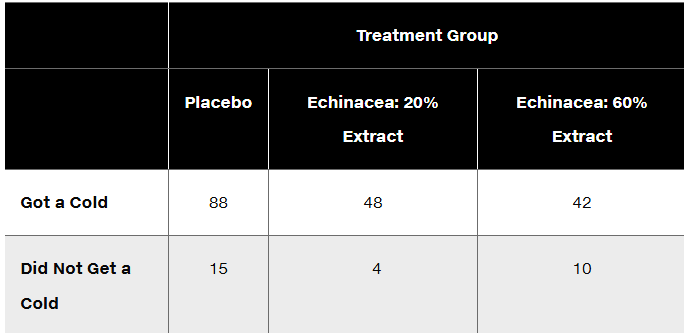
Clinical Trial of Echinacea In a clinical trial of the effectiveness of echinacea for preventing colds, the results in the table below were obtained (based on data from “An Evaluation of Echinacea Angustifolia in Experimental Rhinovirus Infections,” by Turner et al., New England Journal of Medicine, Vol. 353, No. 4). Use a 0.05 significance level to test the claim that getting a cold is independent of the treatment group. What do the results suggest about the effectiveness of echinacea as a prevention against colds?

Accepted Answer

Hello there. Today we're gonna solve the following practice problem together. So first off, let us read the problem and highlight all the key pieces of information that we need to use in order to solve this problem. A teacher wants to know whether the type of reminder given to students affects whether they submit their homework on time. Students were either sent a text reminder or received no reminder. The table below shows the number of students who submitted homework on time and those who did not. On the far right column is not on time. The middle column is on time, and the far left column is text reminder or no reminder for the rows. So for a text reminder on time, there was 18 individuals, and for a text reminder not on time, there was 7 individuals. And for no reminder on time, there was 12 individuals, and no reminder not on time was 13. At the 0.05 significance level, test the claim that submission time is independent of receiving a reminder. What do the results suggest about the effect of sending reminders? Awesome. So it appears for this particular prom, we need to consider the fact that if we have a 0.05 significance level, We need to test the claim that the submission time is independent of receiving a reminder and considering that and all the other information that is provided to us by the prom itself, we need to determine what do the results suggest about the effect of not sending reminders or the effect of sending reminders. So what is the effect of sending reminders. For this particular problem, that's what we're ultimately trying to solve for. So does it matter if you send reminders or doesn't send reminders, etc. So with that in mind, let's read off our multiple choice answers now that we know what we're trying to solve for and see which one might be our final answer. So A is fail to reject the claim there is insufficient evidence to support the claim that reminders affect submission time. Reject the claim, the data suggests that reminders have a significant. effect on submission time. C is reject the claim reminders clearly caused more students to submit homework on time, and then finally D is fail to reject the claim. This confirms that reminders increase homework submission rates. Awesome. So it appears for this particular prompt, our first step that we need to take is we need to state our hypotheses. So let us note that our null hypothesis, which will denote as H0, our null hypothesis will focus on homework submission, and reminder type will be independent of each other. And as for our alternative hypothesis, which will denote as H1, the alternative hypothesis will focus on the fact that homework submission and reminder type are not independent of each other. So now our second step is we need to compute the totals. So for our second step computing the totals, we'll start with our row totals first. So for our row totals, we need to note for text reminders, which I'll call TR for short. We have 18 + 7, and once again we get these values from our table that is provided to us, and 18 + 7 is equal to 25. And are no reminders, which you'll call NR for short. There is 12 + 13, which is going to be equal to 25. And for our column totals, which we'll call CT, We need to note that for on time, which I'll call OT for short, so for on time, it's gonna be 18 + 12, which is going to be equal to 30, and for not on time, we'll call NOT for short, is equal to 7 + 13, which is going to be equal to 20, and then our grand total, which we'll call GT, our grand total will be equal to 50. Fantastic. So now, moving right along here, our third step will be to compute the expected counts. So, in order to do that, we need to recall and use the following equation. We need to note that E is equal to the row total. So the roll total multiplied by the column total, so the row total multiplied by the column total, all divided by the grand total. Fantastic. Now we need to plug in our known variables into this equation to solve for our different variations of our data. So our first variation we need to solve for is for when a text is sent on time, so TOT, so text sent on time, so text on time. So when they send a text message and then they turn their homework in on time, and this is equal to when we plug in our known data, 25 multiplied by 30, divided by 50, which will be equal to 15.0. And for our next condition, so when they send a text and they submit their homework, not on time, so TNOT, so text not on time. So text not on time. In this case, our data points will be 25 multiplied by 20, divided by 50, which is going to be equal to 10. And No reminder. On time, so no reminder and they turn their homework in on time. We'll call this NROT. So no reminder and they turn their homework in on time. When we plug in our known data points, it'll be 25 multiplied by 30 divided by 50, which is equal to 15.0. And finally, No reminder and not on time. So when they are sent no reminder and they don't turn their homework on time, we'll call this NRNOT. And this is equal to 25 multiplied by 20 divided by 50, which when you plug into our calculator, we will get 10. Fantastic. So now, moving right along, our fourth step is we need to compute the G squared statistics. So let us note that G2 is equal to sigma, the sum. Of O minus E to the power 2 divided by E. Where, when we plug in our different data points, we need to note that for when there's a text on time is equal to when we plug in our known data points, 18 minus 15 squad, divided by 15 is going to be equal to when we plug it into our calculator and round the three decial places, 0.600. And our text, when they send a text and it's not on time, it's gonna be equal to parentheses 7 minus 10 to the power of 2 divided by 10, which is equal to, once again, rounding to three deci points, 0.900, and no reminder and it's the homework is on time, it's going to be equal to And let's move this down slightly since we're. A little bit crammed for space here. So once again, to quickly note here, so this is when no reminder is sent and the homework is on time, and this will be equal to parentheses 12 minus 15 2 divided by 15, which is going to be equal to when we plug it into our calculator and round to three decial places, 0.600. Fantastic. Moving right along here. So when no reminder is sent and the homework is not on time, it will be equal to parentheses 13 minus 10 to 2, divided by 10, which is equal to, once again, rounding the three decimal places, 0.900. So that will mean that the G square total will be 0.600 plus 0.900 plus 0.600 plus 0.900, which will be equal to 3.000. Once again, rounding the three decimal places. So now, our 5th and final step is we need to find the critical value. So the degrees of freedom, we'll call this DF for short. So the degrees of freedom is equal to the rows, which I'll call R, are rows. 1 multiplied by our columns, which is called C1, which is equal to 2. And once again, it's rows minus 1, multiplied by columns minus 1, which is going to be equal to 2 minus 1, multiplied by 2 minus 1, which is going to be simply equal to 1. So that means that from the G square table, when we have a significance alpha is equal to 0.05, that would mean that the critical value, which I'll call CV for short, the critical value is approximately equal to 3.841. So now, our 6th step. we need to compare and conclude make our final conclusions. So we need to note that since 3.000 is less than 3.841, we fail to reject the null hypothesis, so I'll put a big red X since we Fail to reject the null hypothesis, so that means in conclusion, there is not enough evidence at the 0.05 significance level to conclude that receiving a reminder affects homework submission time, and this suggests that text reminders may not significantly influence whether students turn in homework on time. So going back to look at our multiple choice answers, that will mean that our final answer, without a doubt has to be multiple choice answer letter A, which once again is fail to reject the claim, there is insufficient evidence to support the claim that reminders affect submission time. Thank you so much for watching. Hopefully that helped, and I can't wait to see you in the next video. Bye.

Key Concepts

Hypothesis Testing

Chi-Square Test of Independence

Significance Level

Watch next