HIC Measurements Listed below are head injury criterion (HIC) ...

Question

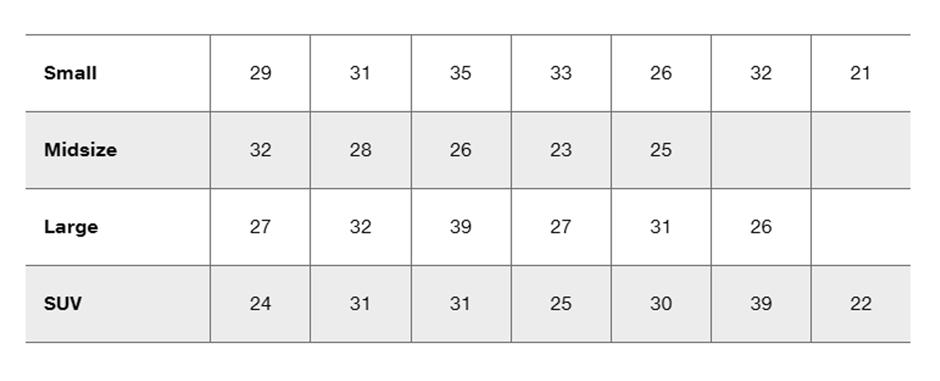
HIC Measurements Listed below are head injury criterion (HIC) measurements from crash tests of small, midsize, large, and SUV vehicles. In using the Kruskal-Wallis test, we must rank all of the data combined, and then we must find the sum of the ranks for each sample. Find the sum of the ranks for each of the four samples.

Table of HIC measurements from crash tests for small, midsize, large, and SUV vehicles.

Accepted Answer

Below there today we're gonna solve the following practice problem together. So first off, let us read the problem and highlight all the key pieces of information that we need to use in order to solve this problem. A scientist records the reaction times in units of milliseconds of participants from 4 age groups teens, 20s, 30s, and 40s. The data is as follows. The teen group has 220, 230, 240, 235, 225. The twenties group has 210, 225, 235, 245, 220. The 30s group has 215, 230, 245, 250, 235. The 40s group has 205, 250, 255, 240, 230. Using a Chris Wallace test, what is the sum of the ranks for the 30s group? Awesome. So it sounds like for this particular problem we're asked to use the Criscoll Wallace test to determine what the sum of the ranks for the 30s group is, and that is our final answer that we're ultimately trying to solve for. So with that in mind, let us read off our multiple choice answers to see what our final answer might be. A is 23.0, B is 59.0, C is 21.0, and D is 17.5. Awesome. So our first step. Or rather, you can combine steps. So our first step is we need to combine all of our reaction times for all age groups, and then we need to put them in ascending order. So once we combine all of our terms and then we sort the values in ascending order, meaning from smallest value to largest value, we should obtain the following. When we put them in order from smallest to largest values. So when we do that we will get 205, 210, 215, 220, 220, 225, 225, 230, 230, 230, 235, 235, 235, 240, 240, 245, 245, 250, 250, and 255. Awesome. So now, Our second major step is we need to assign ranks with tied value sharing the average ranks. So I've gone ahead in order to make this more organized, I've gone ahead and created a data table for us to refer to. So once again, what step we're trying to do to reiterate, is we're assigning ranks, each with tied values sharing the average ranks. So in our far left column, we have our reaction time, and then on the right column, we have the rank. And for our rank going down our column we have 1.0 going up to 20, and for our reaction times we have 205, 210, 215, 220, 225, 230, 235, 240, 245, 250, and 255. With its corresponding rank value, which in order we have a rank once again from 1.0, 1.2, 1.3, 4.5, 6.5, 9.0, 12.0, 14.5, 16.5, 18.5, and 20. Awesome. So those are ranks. So now, our 3rd step. is we need to identify the ranks of the values in the 30s group. So we have 215, which is associated with 3. Then we have 230, which is associated with 9.0. Then we have 245, which is associated with 16.5. Once again, these are different rank values. Then we have 250, which is associated with, once again, 250 is associated with the rank number. 18.5 and then finally, 235 is associated with 12.0. Fantastic. So, moving right along here, we now need to Calculate the sum of the ranks, that's our 4th and final answer, so we need to take. 3 plus 9.0 + 16.5 plus 18.5. And once again, we're taking the sum of our ranks, so 3 + 9.0 plus 16.5 plus 18.5 plus 12.0, which will mean sum those values together, meaning we add them all together, we will get 59.0, when we round to one decimal place. And that is our final answer because once again we had to round to one decimal place to match our multiple choice answers, and that's it. We've officially solved for this problem. Hooray, we did it. So going back to look at our multiple choice answers, that would Mean, without a doubt that our final answer has to be multiple choice answer letter B, which once again is 59.0. Thank you so much for watching. Hopefully that helped, and I can't wait to see you in the next video. Bye.

Key Concepts

Kruskal-Wallis Test

Ranking Data

Sum of Ranks

Watch next