Claim of “At Least” or “At Most”

How do the following results change?

a. Chapter Problem claim is changed to this: “At least 50% of Internet users utilize two-factor authentication to protect their online data.”

Testing Claims About Proportions

In Exercises 9–32, test the given claim. Identify the null hypothesis, alternative hypothesis, test statistic, P-value, or critical value(s), then state the conclusion about the null hypothesis, as well as the final conclusion that addresses the original claim. Use the P-value method unless your instructor specifies otherwise. Use the normal distribution as an approximation to the binomial distribution, as described in Part 1 of this section.

Medical Malpractice In a study of 1228 randomly selected medical malpractice lawsuits, it was found that 856 of them were dropped or dismissed (based on data from the Physicians Insurers Association of America). Use a 0.01 significance level to test the claim that most medical malpractice lawsuits are dropped or dismissed. Should this be comforting to physicians?

Statistical Literacy and Critical Thinking

In Exercises 1–4, use the results from a Hankook Tire Gauge Index survey of a simple random sample of 1020 adults. Among the 1020 respondents, 86% rated themselves as above average drivers. We want to test the claim that more than 3/4 of adults rate themselves as above average drivers.

Number and Proportions

b. Identify the sample proportion and use the symbol that represents it.

Statistical Literacy and Critical Thinking

In Exercises 1–4, use the results from a Hankook Tire Gauge Index survey of a simple random sample of 1020 adults. Among the 1020 respondents, 86% rated themselves as above average drivers. We want to test the claim that more than 3/4 of adults rate themselves as above average drivers.

Number and Proportions

c. For the hypothesis test, identify the value used for the population proportion and use the symbol that represents it.

Statistical Literacy and Critical Thinking

In Exercises 1–4, use the results from a Hankook Tire Gauge Index survey of a simple random sample of 1020 adults. Among the 1020 respondents, 86% rated themselves as above average drivers. We want to test the claim that more than 3/4 of adults rate themselves as above average drivers.

Null and Alternative Hypotheses and Test Statistic

a. Identify the null hypothesis and the alternative hypothesis.

Statistical Literacy and Critical Thinking

In Exercises 1–4, use the results from a Hankook Tire Gauge Index survey of a simple random sample of 1020 adults. Among the 1020 respondents, 86% rated themselves as above average drivers. We want to test the claim that more than 3/4 of adults rate themselves as above average drivers.

Null and Alternative Hypotheses and Test Statistic

b. Find the value of the test statistic.

Statistical Literacy and Critical Thinking

In Exercises 1–4, use the results from a Hankook Tire Gauge Index survey of a simple random sample of 1020 adults. Among the 1020 respondents, 86% rated themselves as above average drivers. We want to test the claim that more than 3/4 of adults rate themselves as above average drivers.

Requirements Are the requirements of the hypothesis test all satisfied? Explain.

Testing Claims About Proportions

In Exercises 9–32, test the given claim. Identify the null hypothesis, alternative hypothesis, test statistic, P-value, or critical value(s), then state the conclusion about the null hypothesis, as well as the final conclusion that addresses the original claim. Use the P-value method unless your instructor specifies otherwise. Use the normal distribution as an approximation to the binomial distribution, as described in Part 1 of this section.

Internet Use A random sample of 5005 adults in the United States includes 751 who do not use the Internet (based on three Pew Research Center polls). Use a 0.05 significance level to test the claim that the percentage of U.S. adults who do not use the Internet is now less than 48%, which was the percentage in the year 2000. If there appears to be a difference, is it dramatic?

Testing Claims About Proportions

In Exercises 9–32, test the given claim. Identify the null hypothesis, alternative hypothesis, test statistic, P-value, or critical value(s), then state the conclusion about the null hypothesis, as well as the final conclusion that addresses the original claim. Use the P-value method unless your instructor specifies otherwise. Use the normal distribution as an approximation to the binomial distribution, as described in Part 1 of this section.

Births A random sample of 860 births in New York State included 426 boys. Use a 0.05 significance level to test the claim that 51.2% of newborn babies are boys. Do the results support the belief that 51.2% of newborn babies are boys?

Testing Claims About Proportions

In Exercises 9–32, test the given claim. Identify the null hypothesis, alternative hypothesis, test statistic, P-value, or critical value(s), then state the conclusion about the null hypothesis, as well as the final conclusion that addresses the original claim. Use the P-value method unless your instructor specifies otherwise. Use the normal distribution as an approximation to the binomial distribution, as described in Part 1 of this section.

Online Friends A Pew Research Center poll of 1060 teens aged 13 to 17 showed that 57% of them have made new friends online. Use a 0.01 significance level to test the claim that half of all teens have made new friends online.

Testing Claims About Proportions

In Exercises 9–32, test the given claim. Identify the null hypothesis, alternative hypothesis, test statistic, P-value, or critical value(s), then state the conclusion about the null hypothesis, as well as the final conclusion that addresses the original claim. Use the P-value method unless your instructor specifies otherwise. Use the normal distribution as an approximation to the binomial distribution, as described in Part 1 of this section.

Belief in Ghosts In a Harris Interactive poll of 2250 adults, 42% of the respondents said that they believe in ghosts. Use a 0.01 significance level to test the claim that more than of adults believe in ghosts.

Using Confidence Intervals to Test Hypotheses When analyzing the last digits of telephone numbers in Port Jefferson, it is found that among 1000 randomly selected digits, 119 are zeros. If the digits are randomly selected, the proportion of zeros should be 0.1.

a. Use the critical value method with a 0.05 significance level to test the claim that the proportion of zeros equals 0.1.

Using Confidence Intervals to Test Hypotheses When analyzing the last digits of telephone numbers in Port Jefferson, it is found that among 1000 randomly selected digits, 119 are zeros. If the digits are randomly selected, the proportion of zeros should be 0.1.

b. Use the P-value method with a 0.05 significance level to test the claim that the proportion of zeros equals 0.1.

Using Confidence Intervals to Test Hypotheses When analyzing the last digits of telephone numbers in Port Jefferson, it is found that among 1000 randomly selected digits, 119 are zeros. If the digits are randomly selected, the proportion of zeros should be 0.1.

c. Use the sample data to construct a 95% confidence interval estimate of the proportion of zeros. What does the confidence interval suggest about the claim that the proportion of zeros equals 0.1?

Using Confidence Intervals to Test Hypotheses When analyzing the last digits of telephone numbers in Port Jefferson, it is found that among 1000 randomly selected digits, 119 are zeros. If the digits are randomly selected, the proportion of zeros should be 0.1.

d. Compare the results from the critical value method, the P-value method, and the confidence interval method. Do they all lead to the same conclusion?

Statistical Literacy and Critical Thinking

In Exercises 1–4, use the results from a Hankook Tire Gauge Index survey of a simple random sample of 1020 adults. Among the 1020 respondents, 86% rated themselves as above average drivers. We want to test the claim that more than 3/4 of adults rate themselves as above average drivers.

Number and Proportions

a. Identify the actual number of respondents who rated themselves as above average drivers.

Using Technology

In Exercises 5–8, identify the indicated values or interpret the given display. Use the normal distribution as an approximation to the binomial distribution, as described in Part 1 of this section. Use a 0.05 significance level and answer the following:

a. Is the test two-tailed, left-tailed, or right-tailed?

b. What is the test statistic?

c. What is the P-value?

d. What is the null hypothesis, and what do you conclude about it?

e. What is the final conclusion?

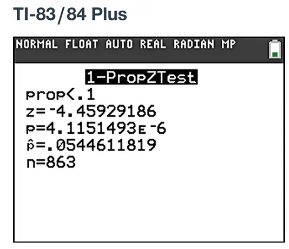
Adverse Reactions to Drug The drug Lipitor (atorvastatin) is used to treat high cholesterol. In a clinical trial of Lipitor, 47 of 863 treated subjects experienced headaches (based on data from Pfizer). The accompanying TI-83/84 Plus calculator display shows results from a test of the claim that fewer than 10% of treated subjects experience headaches.

Exact Method For each of the three different methods of hypothesis testing (identified in the left column), enter the P-values corresponding to the given alternative hypothesis and sample data. Use a 0.05 significance level. Note that the entries in the last column correspond to the Chapter Problem. How do the results agree with the large sample size?

Test Statistic and Critical Value The statistics for the sample data in Exercise 1 are n = 15, x_bar = 6.133333, and s = 8.862978, where the units are millions of dollars. Find the test statistic and critical value(s) for a test of the claim that the salaries are from a population with a mean greater than 5 million dollars. Assume that a 0.05 significance level is used.

Finding P-values

In Exercises 5–8, either use technology to find the P-value or use Table A-3 to find a range of values for the P-value. Based on the result, what is the final conclusion?

Weights of Quarters The claim is that weights (grams) of quarters made after 1964 have a mean equal to 5.670 g as required by mint specifications. The sample size is and the test statistic is t = -3.135.

Finding P-values

In Exercises 5–8, either use technology to find the P-value or use Table A-3 to find a range of values for the P-value. Based on the result, what is the final conclusion?

Cotinine in Smokers The claim is that smokers have a mean cotinine level greater than the level of 2.84 ng/mL found for nonsmokers. (Cotinine is used as a biomarker for exposure to nicotine.) The sample size is n = 902 and the test statistic is t = 56.319.

Testing Claims About Variation

In Exercises 5–16, test the given claim. Identify the null hypothesis, alternative hypothesis, test statistic, P-value, or critical value(s), then state the conclusion about the null hypothesis, as well as the final conclusion that addresses the original claim. Assume that a simple random sample is selected from a normally distributed population.

Minting of Pennies Data Set 40 “Coin Weights” lists weights (grams) of pennies minted after 1983. Here are the statistics for those weights: n = 37, xbar = 2.49910 g, s = 0.01648 g . Use a 0.05 significance level to test the claim that the sample is from a population of pennies with weights having a standard deviation greater than 0.01000 g.

Testing Claims About Variation

In Exercises 5–16, test the given claim. Identify the null hypothesis, alternative hypothesis, test statistic, P-value, or critical value(s), then state the conclusion about the null hypothesis, as well as the final conclusion that addresses the original claim. Assume that a simple random sample is selected from a normally distributed population.

Bank Lines The Jefferson Valley Bank once had a separate customer waiting line at each teller window, but it now has a single waiting line that feeds the teller windows as vacancies occur. The standard deviation of customer waiting times with the old multiple-line configuration was 1.8 min. Listed below is a simple random sample of waiting times (minutes) with the single waiting line. Use a 0.05 significance level to test the claim that with a single waiting line, the waiting times have a standard deviation less than 1.8 min. What improvement occurred when banks changed from multiple waiting lines to a single waiting line?

6.5 6.6 6.7 6.8 7.1 7.3 7.4 7.7 7.7 7.7

Testing Claims About Variation

In Exercises 5–16, test the given claim. Identify the null hypothesis, alternative hypothesis, test statistic, P-value, or critical value(s), then state the conclusion about the null hypothesis, as well as the final conclusion that addresses the original claim. Assume that a simple random sample is selected from a normally distributed population.

Birth Weights A simple random sample of birth weights of 30 girls has a standard deviation of 829.5 g. Use a 0.01 significance level to test the claim that birth weights of girls have the same standard deviation as birth weights of boys, which is 660.2 g (based on Data Set 6 “Births” in Appendix B).

Minting Dollar Coins For the sample data from Exercise 1, we get a P-value of 0.0041 when testing the claim that σ < 0.04000 g.

What should we conclude about the null hypothesis?

What should we conclude about the original claim?

What do these results suggest about the new minting process?

Finding Critical Values of (chi)^2 For large numbers of degrees of freedom, we can approximate critical values of as follows:

(chi)^2 = (1/2)(z + sqrt(2k-1))

Here k is the number of degrees of freedom and z is the critical value(s) found from technology or Table A-2. In Exercise 12 “Spoken Words” we have df = 55, so Table A-4 does not list an exact critical value. If we want to approximate a critical value of (chi)^2 in the right-tailed hypothesis test with α = 0.01 and a sample size of 56, we let k =55 with z = 2.33 (or the more accurate value of z = 2.326348 found from technology). Use this approximation to estimate the critical value of for Exercise 12. How close is it to the critical value of (chi)^2 = 82.292 obtained by using Statdisk and Minitab?

Testing Claims About Variation

In Exercises 5–16, test the given claim. Identify the null hypothesis, alternative hypothesis, test statistic, P-value, or critical value(s), then state the conclusion about the null hypothesis, as well as the final conclusion that addresses the original claim. Assume that a simple random sample is selected from a normally distributed population.

Pulse Rates of Men A simple random sample of 153 men results in a standard deviation of 11.3 beats per minute (based on Data Set 1 “Body Data” in Appendix B). The normal range of pulse rates of adults is typically given as 60 to 100 beats per minute. If the range rule of thumb is applied to that normal range, the result is a standard deviation of 10 beats per minute. Use the sample results with a 0.05 significance level to test the claim that pulse rates of men have a standard deviation equal to 10 beats per minute; see the accompanying StatCrunch display for this test. What do the results indicate about the effectiveness of using the range rule of thumb with the “normal range” from 60 to 100 beats per minute for estimating in this case?

RESAMPLING

a. In general, what does it mean to “resample” the following data set consisting of wait times (minutes) of customers waiting in line for the Space Mountain ride at Walt Disney World: 50, 25, 75, 35, 50?

RESAMPLING

c. When testing a claim about a proportion or mean or standard deviation, what is an important advantage of using a resampling method instead of the parametric method described in the preceding sections of this chapter?

At Least As Extreme A random sample of 860 births in New York State included 426 boys, and that sample is to be used for a test of the common belief that the proportion of male births in the population is equal to 0.512.

a. In testing the common belief that the proportion of male babies is equal to 0.512, identify the values of p^ and p.