Back
BackProblem 7.3.28
Dive Duration An oceanographer claims that the mean dive duration of a North Atlantic right whale is 11.5 minutes. A random sample of 34 dive durations has a mean of 12.2 minutes and a standard deviation of 2.2 minutes. Is there enough evidence to reject the claim at α=0.10?
Problem 7.3.26
Hypothesis Testing Using Rejection Regions In Exercises 19–26, (a) identify the claim and state H0 and Ha, (b) find the critical value(s) and identify the rejection region(s), (c) find the standardized test statistic t, (d) decide whether to reject or fail to reject the null hypothesis, and (e) interpret the decision in the context of the original claim. Assume the population is normally distributed.
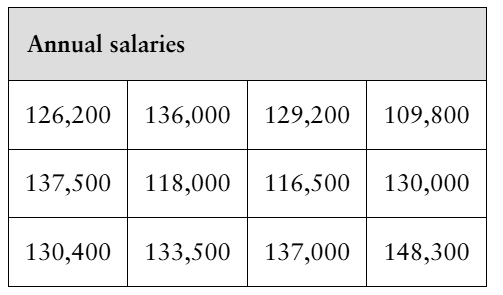
Annual Salary An employment information service claims the mean annual salary for senior level statisticians is more than $124,000. The annual salaries (in dollars) for a random sample of 12 senior level statisticians are shown in the table at the left. At α=0.01, is there enough evidence to support the claim that the mean salary is more than $124,000?
Problem 7.3.24
Hypothesis Testing Using Rejection Regions In Exercises 19–26, (a) identify the claim and state H0 and Ha, (b) find the critical value(s) and identify the rejection region(s), (c) find the standardized test statistic t, (d) decide whether to reject or fail to reject the null hypothesis, and (e) interpret the decision in the context of the original claim. Assume the population is normally distributed.
Lead Levels As part of your work for an environmental awareness group, you want to test a claim that the mean amount of lead in the air in U.S. cities is less than 0.032 microgram per cubic meter. You find that the mean amount of lead in the air for a random sample of 56 U.S. cities is 0.021 microgram per cubic meter and the standard deviation is 0.034 microgram per cubic meter. At α=0.01, can you support the claim?
Problem 7.3.21
Hypothesis Testing Using Rejection Regions In Exercises 19–26, (a) identify the claim and state H0 and Ha, (b) find the critical value(s) and identify the rejection region(s), (c) find the standardized test statistic t, (d) decide whether to reject or fail to reject the null hypothesis, and (e) interpret the decision in the context of the original claim. Assume the population is normally distributed.
Credit Card Debt A credit reporting agency claims that the mean credit card debt in Colorado is greater than $5540 per borrower. You want to test this claim. You find that a random sample of 30 borrowers has a mean credit card debt of $5594 per person and a standard deviation of $597 per person. At , can you support the claim α=0.05?
Problem 7.3.2
Explain how to use a t-test to test a hypothesized mean mu when sigma is unknown. What assumptions are necessary?
Problem 7.3.3
In Exercises 3–8, find the critical value(s) and rejection region(s) for the type of t-test with level of significance alpha and sample size n.
Left-tailed test, α=0.10, n=20
Problem 7.3.8
In Exercises 3–8, find the critical value(s) and rejection region(s) for the type of t-test with level of significance alpha and sample size n.
Left-tailed test, α=0.10, n=38
Problem 7.3.33
Writing You are testing a claim and incorrectly use the standard normal sampling distribution instead of the t-sampling distribution, mistaking the sample standard deviation for the population standard deviation. Does this make it more or less likely to reject the null hypothesis? Is this result the same no matter whether the test is left-tailed, right-tailed, or two-tailed? Explain your reasoning.
Problem 7.3.6
In Exercises 3–8, find the critical value(s) and rejection region(s) for the type of t-test with level of significance alpha and sample size n.
Right-tailed test, α=0.01, n=31
Problem 7.31
In Exercises 29 –34, find the critical value(s) and rejection region(s) for the type of t-test with level of significance α and sample size n.
Right-tailed test, α=0.02, n=63
Problem 7.4.2
Explain how to test a population proportion p.
Problem 7.4.5
In Exercises 3–8, find the critical value(s) and rejection region(s) for the type of t-test with level of significance alpha and sample size n.
Right-tailed test, α=0.05, n=23
Problem 7.4.7
In Exercises 3–8, find the critical value(s) and rejection region(s) for the type of t-test with level of significance alpha and sample size n.
Two-tailed test, α=0.05, n=27
Problem 7.4.9b
Graphical Analysis In Exercises 9–12, state whether each standardized test statistic t allows you to reject the null hypothesis. Explain.
b. t = 0
Problem 7.4.9c
Graphical Analysis In Exercises 9–12, state whether each standardized test statistic t allows you to reject the null hypothesis. Explain.
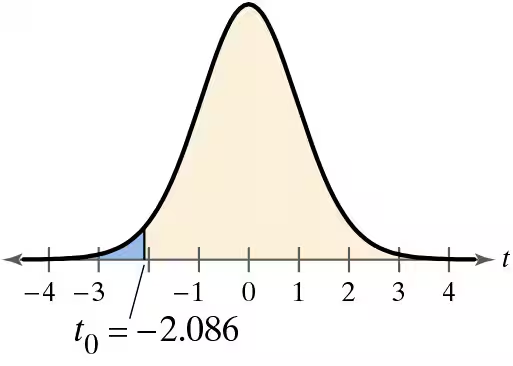
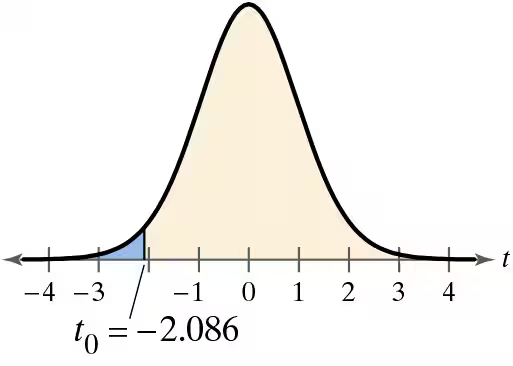
c. t = -2.096
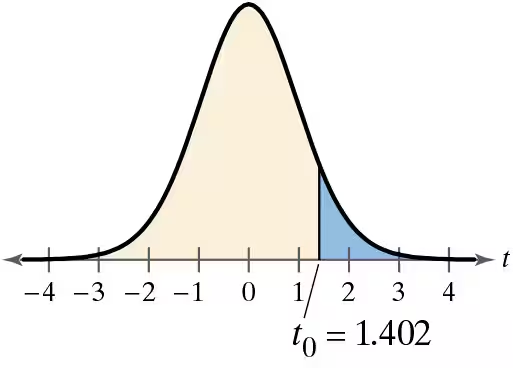
Problem 7.4.10a
Graphical Analysis In Exercises 9–12, state whether each standardized test statistic t allows you to reject the null hypothesis. Explain.
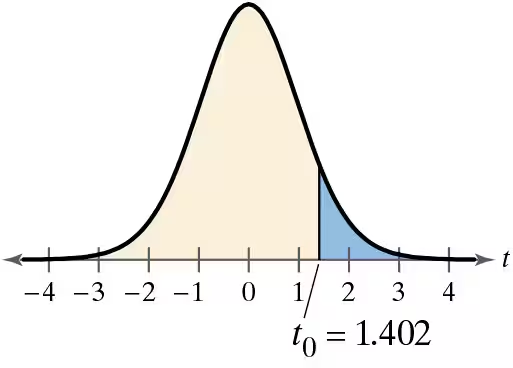
a. t = 1.4
Problem 7.4.10b
Graphical Analysis In Exercises 9–12, state whether each standardized test statistic t allows you to reject the null hypothesis. Explain.
b. t = 1.42
Problem 7.4.6
In Exercises 3–6, determine whether a normal sampling distribution can be used. If it can be used, test the claim.
Claim: p > 0.70, α=0.04. Sample statistics: p_hat = 0.64, n=225
Problem 7.4.4
In Exercises 3–6, determine whether a normal sampling distribution can be used. If it can be used, test the claim.
Claim: p ≥0.48, α=0.08. Sample statistics: p_hat = 0.40, n=90
Problem 7.4.8
Hypothesis Testing Using Rejection Regions In Exercises 7–12, (a) identify the claim and state H0 and Ha, (b) find the critical value(s) and identify the rejection region(s), (c) find the standardized test statistic z, (d) decide whether to reject or fail to reject the null hypothesis, and (e) interpret the decision in the context of the original claim.
Vaccinations In 2021, a reporter claims that at least 55% of U.S. adults feel that COVID-19 vaccinations should be required for high school students to attend school in the fall. In a random sample of 200 U.S. adults, 56% feel that COVID-19 vaccinations should be required for high school students to attend school in the fall. At α=0.10, is there enough evidence to reject the reporter’s claim?
Problem 7.4.10
Hypothesis Testing Using Rejection Regions In Exercises 7–12, (a) identify the claim and state H0 and Ha, (b) find the critical value(s) and identify the rejection region(s), (c) find the standardized test statistic z, (d) decide whether to reject or fail to reject the null hypothesis, and (e) interpret the decision in the context of the original claim.
Working Students An education researcher claims that 65% of full-time college students work year-round. In a random sample of 105 college students, 66 say they work year-round. At α=0.10, is there enough evidence to reject the researcher’s claim?
Problem 7.4.12
Hypothesis Testing Using Rejection Regions In Exercises 7–12, (a) identify the claim and state H0 and Ha, (b) find the critical value(s) and identify the rejection region(s), (c) find the standardized test statistic z, (d) decide whether to reject or fail to reject the null hypothesis, and (e) interpret the decision in the context of the original claim.
Changing Jobs A researcher claims that 40% of U.S. adults would consider changing jobs. In a random sample of 50 U.S. adults, 25 say they would consider changing jobs. At α=0.10, is there enough evidence to reject the researcher’s claim?
Problem 7.4.16
Hypothesis Testing Using a P-Value In Exercises 13–16, (a) identify the claim and state H0 and Ha, (b) use technology to find the P-value, (c) decide whether to reject or fail to reject the null hypothesis, and (d) interpret the decision in the context of the original claim.
Stray Cats An animal advocate claims that 25% of U.S. households have taken in a stray cat. In a random sample of 500 U.S. households, 105 say they have taken in a stray cat. At α=0.05, is there enough evidence to reject the advocate’s claim?
Problem 7.4.11
Hypothesis Testing Using Rejection Regions In Exercises 7–12, (a) identify the claim and state H0 and Ha, (b) find the critical value(s) and identify the rejection region(s), (c) find the standardized test statistic z, (d) decide whether to reject or fail to reject the null hypothesis, and (e) interpret the decision in the context of the original claim.
Nursing A patient care manager claims that more than half of all nurses feel they became better professionals during the coronavirus pandemic. In a random sample of 300 nurses, 174 say they became better professionals during the pandemic. At α=0.01, is there enough evidence to support the manager’s claim?
Problem 7.4.17
use the figure at the left, which suggests what adults think about protecting the environment.
[Image]
Are People Concerned About Protecting the Environment? You interview a random sample of 100 adults. The results of the survey show that 58% of the adults said they live in ways that help protect the environment some of the time. At α=0.05, can you reject the claim that at least 64% of adults make an effort to live in ways that help protect the environment some of the time?
Problem 7.4.3
In Exercises 3–6, determine whether a normal sampling distribution can be used. If it can be used, test the claim.
Claim: p <0.12, α=0.01. Sample statistics: p_hat = 0.10, n=40
Problem 7.4.5a
In Exercises 3–6, determine whether a normal sampling distribution can be used. If it can be used, test the claim.
Claim: p ≠0.15, α=0.05. Sample statistics: p_hat = 0.12, n=500
Problem 7.5.4
Describe the difference between calculating the standardized test statistic, Z^2, for a chi-square test for variance and a chi-square test for standard deviation.
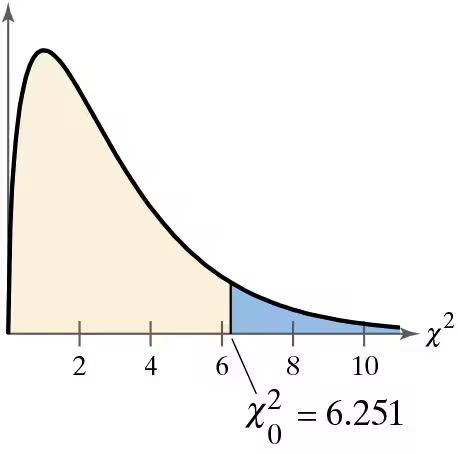
Problem 7.5.13a
Graphical Analysis In Exercises 13 and 14, state whether each standardized test statistic X^2 allows you to reject the null hypothesis. Explain.
a. X^2=2.091
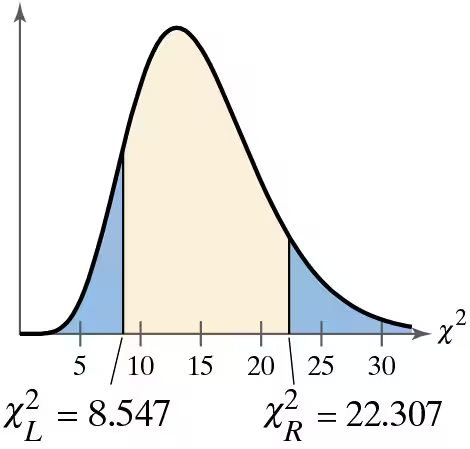
Problem 7.5.14b
Graphical Analysis In Exercises 13 and 14, state whether each standardized test statistic X^2 allows you to reject the null hypothesis. Explain.
b. X^2=23.309