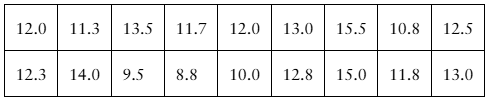
Constructing a Confidence Interval In Exercises 25–28, use the data set to (c) construct a 99% confidence interval for the population mean. Assume the population is normally distributed.

Homework The weekly time spent (in hours) on homework for 18 randomly selected high school students

Finite Population Correction Factor In Exercises 57 and 58, use the information below.

In this section, you studied the construction of a confidence interval to estimate a population mean. In each case, the underlying assumption was that the sample size n was small in comparison to the population size N. When n ≥ 0.05N however, the formula that determines the standard error of the mean needs to be adjusted, as shown below.

[IMAGE]

Recall from the Section 5.4 exercises that the expression sqrt[(N-n)/(n-1)] is called a finite population correction factor. The margin of error is

[IMAGE]

Use the finite population correction factor to construct each confidence interval for the population mean.

c. c = 0.95, xbar = 40.3, σ = 0.5, N = 300, n = 68.

When all other quantities remain the same, how does the indicated change affect the width of a confidence interval? Explain.

c. Increase in the population standard deviation

In a survey of 2096 U.S. adults, 1740 think football teams of all levels should require players who suffer a head injury to take a set amount of time off from playing to recover. (Adapted from The Harris Poll)

d. Find the minimum sample size needed to estimate the population proportion at the 99% confidence level to ensure that the estimate is accurate within 3% of the population proportion.