Back
BackProblem 6.3.18a
Senate Filibuster You wish to estimate, with 99% confidence, the population proportion of U.S. adults who disapprove of the U.S Senate’s use of the filibuster. Your estimate must be accurate within 2% of the population proportion.
a. No preliminary estimate is available. Find the minimum sample size needed.
Problem 6.3.32
Translating Statements In Exercises 29–34, translate the statement into a confidence interval. Approximate the level of confidence.
In a survey of 880 unmarried U.S. adults who are living with a partner, 73% say love was a major reason why they decided to move in together. The survey’s margin of error is ±4.8%. (Source: Pew Research Center)
Problem 6.3.33
Translating Statements In Exercises 29–34, translate the statement into a confidence interval. Approximate the level of confidence.
In a survey of 2094 U.S. adults who have used an online dating app, 57% said their personal experience with online dating was positive. The survey’s margin of error is ±3.6%. (Source: Pew Research Center)
Problem 6.3.35
Why Check It? Why is it necessary to check that np^ ≥ 5 and nq^ ≥ 5?
Problem 6.3.34
Translating Statements In Exercises 29–34, translate the statement into a confidence interval. Approximate the level of confidence.
In a survey of 1052 parents of children ages 8–14, 68% say they are willing to get a second or part-time job to pay for their children’s college education, and 42% say they lose sleep worrying about college costs. The survey’s margin of error is ±3%. (Source: T. Rowe Price Group, Inc.)
Problem 6.3.27
Constructing Confidence Intervals In Exercises 27 and 28, use the figure, which shows the results of a survey in which 1021 U.S. adults were asked whether they see each of the possible threats to the vital interests of the United States as a critical threat in the next 10 years. (Source: Gallup)
Critical Threats Construct a 95% confidence interval for the population proportion of U.S. adults who gave each response.
Problem 6.3.3
"Finding p^ and q^ In Exercises 3 – 6, let p be the population proportion for the situation. Find point estimates of p and q.
Tax Fraud In a survey of 1040 U.S. adults, 62 have had someone impersonate them to try to claim tax refunds. (Adapted from Pew Research Center)"
Problem 6.3.4
"Finding p^ and q^ In Exercises 3 – 6, let p be the population proportion for the situation. Find point estimates of p and q.
Social Security In a survey of 351 retired Americans, 200 said that they rely on Social Security as major source of income. (Adapted from Gallup)"
Problem 6.4.26
Drug Concentration You are analyzing the times for the drug concentrations to peak in the patients in Exercise 14. The population standard deviation of the times for epinephrine concentrations to peak should be less than 10 minutes. Does the confidence interval you constructed for σ suggest that the variation in the times is at an acceptable level? Explain your reasoning.
Problem 6.4.1
Does a population have to be normally distributed to use the chi-square distribution?
Problem 6.4.2
What happens to the shape of the chi-square distribution as the degrees of freedom increase?
Problem 6.4.6
Finding Critical Values for χ2 In Exercises 3–8, find the critical values χR2 and χL2 for the level of confidence c and sample size n.
c = 0.98, n = 26
Problem 6.4.7
Finding Critical Values for χ2 In Exercises 3–8, find the critical values χR2 and χL2 for the level of confidence c and sample size n.
c = 0.99, n = 30
Problem 6.4.8
Finding Critical Values for χ2 In Exercises 3–8, find the critical values χR2 and χL2 for the level of confidence c and sample size n.
c = 0.80, n = 51
Problem 6.4.9
In Exercises 9–12, construct the indicated confidence intervals for (a) the population variance and (b) the population standard deviation . Assume the sample is from a normally distributed population.
c = 0.95, s^2 = 11.56, n = 30
Problem 6.4.10
In Exercises 9–12, construct the indicated confidence intervals for (a) the population variance and (b) the population standard deviation . Assume the sample is from a normally distributed population.
c = 0.99, s^2 = 0.64, n = 7
Problem 6.4.11
In Exercises 9–12, construct the indicated confidence intervals for (a) the population variance and (b) the population standard deviation . Assume the sample is from a normally distributed population.
c = 0.90, s^2 = 35, n = 18
Problem 6.4.14a
Constructing Confidence Intervals In Exercises 13–24, assume the sample is from a normally distributed population and construct the indicated confidence intervals for (a) the population variance σ^2. Interpret the results.
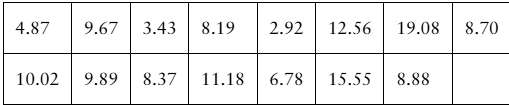
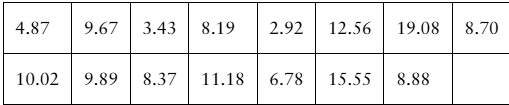
Drug Concentration The times (in minutes) for the drug concentration to peak when the drug epinephrine is injected into 15 randomly selected patients are listed. Use a 90% level of confidence.
Problem 6.4.14b
Constructing Confidence Intervals In Exercises 13–24, assume the sample is from a normally distributed population and construct the indicated confidence intervals for (b) the population standard deviation σ. Interpret the results.
Drug Concentration The times (in minutes) for the drug concentration to peak when the drug epinephrine is injected into 15 randomly selected patients are listed. Use a 90% level of confidence.
Problem 6.4.15a
Constructing Confidence Intervals In Exercises 13–24, assume the sample is from a normally distributed population and construct the indicated confidence intervals for (a) the population variance σ^2. Interpret the results.
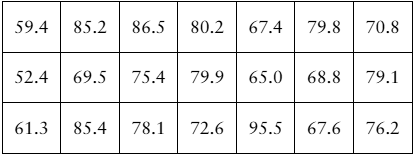
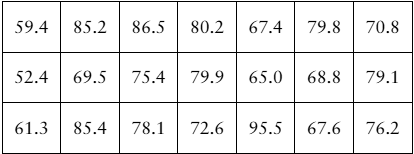
[APPLET] Earnings The annual earnings (in thousands of dollars) of 21 randomly selected level 1 computer hardware engineers are listed. Use a 99% level of confidence. (Adapted from Salary.com)
Problem 6.4.15b
Constructing Confidence Intervals In Exercises 13–24, assume the sample is from a normally distributed population and construct the indicated confidence intervals for (b) the population standard deviation σ. Interpret the results.
[APPLET] Earnings The annual earnings (in thousands of dollars) of 21 randomly selected level 1 computer hardware engineers are listed. Use a 99% level of confidence. (Adapted from Salary.com)
Problem 6.4.18a
Constructing Confidence Intervals In Exercises 13–24, assume the sample is from a normally distributed population and construct the indicated confidence intervals for (a) the population variance σ^2. Interpret the results.
Volleyball The numbers of service aces scored by 15 teams randomly selected from the top 50 NCAA Division I Women’s Volleyball teams for the 2021 season have a sample standard deviation of 26.1. Use an 80% level of confidence. (Source: National Collegiate Athletic Association)
Problem 6.4.18b
Constructing Confidence Intervals In Exercises 13–24, assume the sample is from a normally distributed population and construct the indicated confidence intervals for (a) the population variance σ^2. Interpret the results.
Volleyball The numbers of service aces scored by 15 teams randomly selected from the top 50 NCAA Division I Women’s Volleyball teams for the 2021 season have a sample standard deviation of 26.1. Use an 80% level of confidence. (Source: National Collegiate Athletic Association)
Problem 6.4.21a
Constructing Confidence Intervals In Exercises 13–24, assume the sample is from a normally distributed population and construct the indicated confidence intervals for (a) the population variance σ^2. Interpret the results.
Car Batteries The reserve capacities (in hours) of 18 randomly selected automotive batteries have a sample standard deviation of 0.25 hour. Use an 80% level of confidence.
Problem 6.4.21b
Constructing Confidence Intervals In Exercises 13–24, assume the sample is from a normally distributed population and construct the indicated confidence intervals for (b) the population standard deviation σ. Interpret the results.
Car Batteries The reserve capacities (in hours) of 18 randomly selected automotive batteries have a sample standard deviation of 0.25 hour. Use an 80% level of confidence.
Problem 6.4.22a
Constructing Confidence Intervals In Exercises 13–24, assume the sample is from a normally distributed population and construct the indicated confidence intervals for (a) the population variance σ^2. Interpret the results.
Annual Precipitation The annual precipitation amounts (in inches) of a random sample of 61 years for Chicago, Illinois, have a sample standard deviation of 6.46. Use a 98% level of confidence. (Source: National Oceanic and Atmospheric Administration)
Problem 6.4.22b
Constructing Confidence Intervals In Exercises 13–24, assume the sample is from a normally distributed population and construct the indicated confidence intervals for (b) the population standard deviation σ. Interpret the results.
Annual Precipitation The annual precipitation amounts (in inches) of a random sample of 61 years for Chicago, Illinois, have a sample standard deviation of 6.46. Use a 98% level of confidence. (Source: National Oceanic and Atmospheric Administration)
Problem 6.4.23a
Constructing Confidence Intervals In Exercises 13–24, assume the sample is from a normally distributed population and construct the indicated confidence intervals for (a) the population variance σ^2. Interpret the results.
Drive-Thru Times The times (in seconds) spent by a random sample of 28 customers in the drive-thru of a fast-food restaurant have a sample standard deviation of 56.1. Use a 98% level of confidence.
Problem 6.4.23b
Constructing Confidence Intervals In Exercises 13–24, assume the sample is from a normally distributed population and construct the indicated confidence intervals for (b) the population standard deviation σ. Interpret the results.
Drive-Thru Times The times (in seconds) spent by a random sample of 28 customers in the drive-thru of a fast-food restaurant have a sample standard deviation of 56.1. Use a 98% level of confidence.
Problem 6.4.12
In Exercises 9–12, construct the indicated confidence intervals for (a) the population variance and (b) the population standard deviation . Assume the sample is from a normally distributed population.
c = 0.98, s^2 = 278.1, n =41