Back
BackProblem 3.RS.3b
You work in the security department of a bank’s website. To access their accounts, customers of the bank must create an 8-digit password. It is your job to determine the password requirements for these accounts. Security guidelines state that for the website to be secure, the probability that an 8-digit password is guessed on one try must be less than 1/60^8, assuming all passwords are equally likely.
Your job is to use the probability techniques you have learned in this chapter to decide what requirements a customer must meet when choosing a password, including what sets of characters are allowed, so that the website is secure according to the security guidelines.
3. For additional security, each customer creates a 5-digit PIN (personal identification number). The table on the right shows the 10 most commonly chosen 5-digit PINs. From the table, you can see that more than a third of all 5-digit PINs could be guessed by trying these 10 numbers. To discourage customers from using predictable PINs, you consider prohibiting PINs that use the same digit more than once.
b. Would you decide to prohibit PINs that use the same digit more than once? Explain.
Problem 3.RS.2a
You work in the security department of a bank’s website. To access their accounts, customers of the bank must create an 8-digit password. It is your job to determine the password requirements for these accounts. Security guidelines state that for the website to be secure, the probability that an 8-digit password is guessed on one try must be less than 1/60^8, assuming all passwords are equally likely.
Your job is to use the probability techniques you have learned in this chapter to decide what requirements a customer must meet when choosing a password, including what sets of characters are allowed, so that the website is secure according to the security guidelines.
2. Answering the Question
a. What password requirements would you set? What characters would be allowed?
Problem 3.T.4d
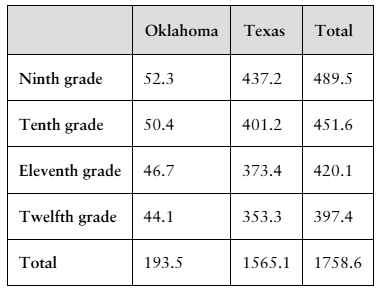
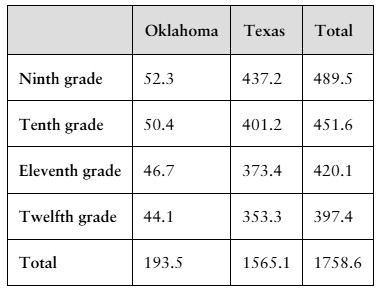
4. The table on the left shows the secondary school student enrollment levels (in thousands by grade) in Oklahoma and Texas schools in a recent year. (Source: U.S. Nation
for Education Statistics)
A student in one of the indicated grades and states is randomly selected. Find the probability of selecting a student who
d. is enrolled in Texas, given that the student is in twelfth grade.
Problem 3.T.5
5. Use technology to randomly select two numbers from 1 to 6. Find the sum and subtract 1 to obtain a total.
a. What is the theoretical probability of each total from 1 to 11?
b. Use this procedure to select 100 totals from 1 to 11. Tally your results and compare them with the probabilities in part (a).
Problem 3.T.2c
A person's building access code is their first and last initials and four digits.
You know a person's first name only, and you know that the last digit is odd. What is the probability of guessing this person's code on the first try?
Problem 3.T.7b
7. There are 16 students giving final presentations in your history course.
b. Presentation subjects are based on the units of the course. Unit B is covered by three students, Unit C is covered by five students, and Units A and D are each covered by four students. How many presentation orders are possible when presentations on
the same unit are indistinguishable from each other?
Problem 3.T.1
Your dorm enters 15 out of 65 plastic numbered ducks in a duck race. The ducks are all dumped into a stream and drift to the finish line. What is the probability that three of your dorm's ducks finish first, second, and third?
Problem 3.T.4a
4. The table on the left shows the secondary school student enrollment levels (in thousands by grade) in Oklahoma and Texas schools in a recent year. (Source: U.S. Nation
for Education Statistics)
A student in one of the indicated grades and states is randomly selected. Find the probability of selecting a student who
a. is in ninth grade.
Problem 3.T.2
2. How many possible variations are there in Mozart's Musical Dice Game minuet? Explain.
Problem 3.Test.5
5. Which event(s) in Exercise 4 can be considered unusual? Explain your reasoning.
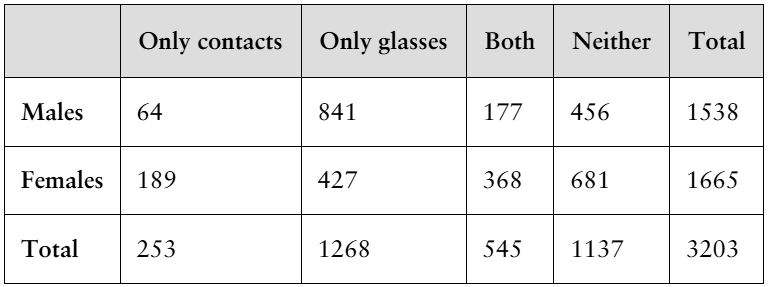
Problem 3.3.26a
26. Eye Survey The table shows the results of a survey that asked 3203 people whether they wore contacts or glasses. A person is selected at random from the sample. Find the probability of each event.
a. The person wears only contacts or only glasses.
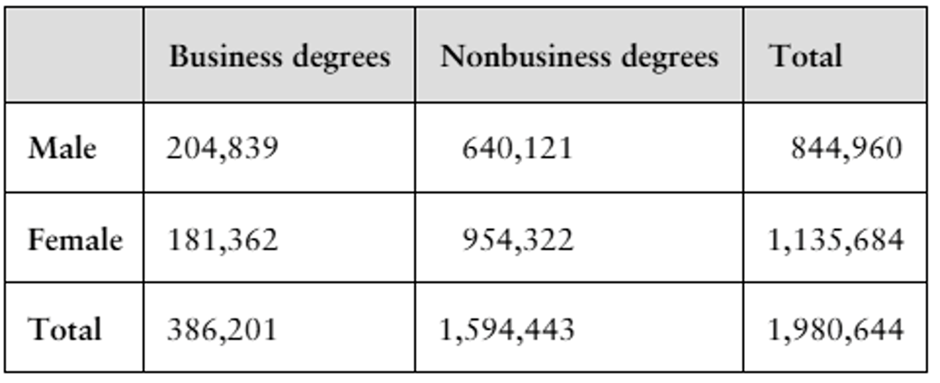
Problem 3.2.7a
Finding Conditional Probabilities In Exercises 7 and 8, use the table to find each conditional probability.
7. Business Degrees The table shows the numbers of male and female students in the United States who received bachelor's degrees in business and nonbusiness fields in a recent year. (Source: National Center for Educational Statistics)
a. Find the probability that a randomly selected bachelor's degree-earning student is male, given that the degree is in business.
Problem 3.1.66a
66. Access Code An access code consists of six characters. For each character, any letter or number can be used, with the exceptions that the first character cannot be 0 and the last two characters must be odd numbers.
a. What is the probability of randomly selecting the correct access code on the first try?
Problem 3.2.25a
Using the Multiplication Rule In Exercises 19-32, use the Multiplication Rule.
25. Best President In a sample of 1500 adult U.S. citizens, 270 said that Barack Obama was the best president in U.S. history. Two adult U.S. citizens are selected at random.
(Adapted from YouGov)
a. Find the probability that both adult U.S. citizens say that Barack Obama was the best president in U.S. history.
Problem 3.2.1a
"1. What is the difference between independent and dependent events?
Problem 3.2.26a
"Using the Multiplication Rule In Exercises 19-32, use the Multiplication Rule.
26. Worst President In a sample of 1500 adult U.S. citizens, 690 said that Donald Trump was the worst president in U.S. history. Three adult U.S. citizens are selected at random.
(Adapted from YouGov)
a. Find the probability that all three adult U.S. citizens say that Donald Trump was the worst president in U.S. history."
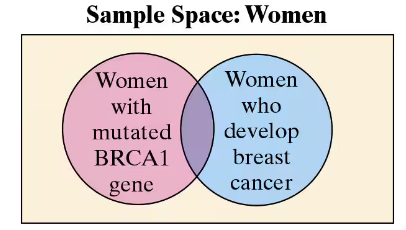
Problem 3.2.21a
"Using the Multiplication Rule In Exercises 19-32, use the Multiplication Rule.
21. BRCA1 Gene Research has shown that approximately 1 woman in 400 carries a mutation of the BRCA1 gene. About 64% of women with this mutation develop breast
cancer. Find the probability that a randomly selected woman will carry the mutation of the BRCA1 gene and will develop breast cancer. (Source: National Cancer Institute)
Problem 3.4.43a
Shuffle Play You use a shuffle playback feature to randomly play songs in a playlist. The playlist of 56 songs includes 15 instrumental songs.
a. What is the probability that the first three songs to play are instrumental songs? (Assume a song cannot be repeated.)
Problem 3.1.87a
87. College Football A stem-and-leaf plot for the numbers of touchdowns allowed by the 127 NCAA Division I Football Bowl Subdivision teams in the 2020-2021 season is shown. Find the probability that a team chosen at random allowed (a) at least 51 touchdowns. Are any of these events unusual? Explain. (Source: National Collegiate Athletic Association)
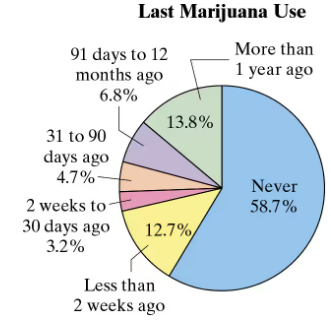
Problem 3.3.20a
Marijuana Use The percent distribution of the last marijuana use (either medical or nonmedical) for a sample of 13,373 college students is shown in the pie chart. Find the
probability of each event. (Source: American College Health Association)
a. Randomly selecting a student who never used marijuana
Problem 3.2.24a
Using the Multiplication Rule In Exercises 19-32, use the Multiplication Rule.
24. Knowing a Person Who Was Murdered In a sample of 11,771 children ages 2 to 17, 8% have lost a friend or relative to murder. Four children are selected at random. (Adapted from University of New Hampshire)
a. Find the probability that all four have lost a friend or relative to murder.
Problem 3.4.50a
50. Investment Committee A company has 200 employees, consisting of 144 women and 56 men. The company wants to select five employees to serve as an investment committee.
a. Use technology to find the number of ways that 5 employees can be selected from 200.
Problem 3.1.2a
2. Determine whether each number could represent the probability of an event. Explain your reasoning. a. 25/25
Problem 3.2.29a
Using the Multiplication Rule In Exercises 19-32, use the Multiplication Rule.
29. In Vitro Fertilization In a recent year, about 1.9% of all infants born in the U.S. were conceived through assisted reproductive technology (ART). Of the ART deliveries, about 26.4% resulted in multiple births. (Source: Morbidity and Mortality Weekly Report)
a. Find the probability that a randomly selected infant was conceived through ART and was part of a multiple birth.
Problem 3.2.28a
"Using the Multiplication Rule In Exercises 19-32, use the Multiplication Rule.
28. Blood Types The probability that a Latinx American person in the United States has type A+ blood is 29%. Four Latinx American people in the United States are selected at random. (Source: American National Red Cross)
a. Find the probability that all four have type A+ blood."
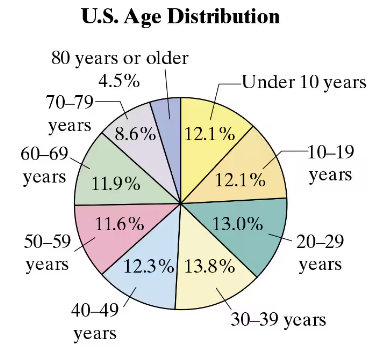
Problem 3.3.19a
U.S. Age Distribution The projected percent distribution of the U.S. population for 2025 is shown in the pie chart. Find the probability of each event. (Source: U.S. Census
Bureau)
a. Randomly selecting someone who is under 10 years old
Problem 3.2.23a
Using the Multiplication Rule In Exercises 19-32, use the Multiplication Rule.
23. Celebrities as Role Models In a sample of 1103 probable voters, three out of four say they would like entertainers to address social and political issues. Two probable voters are selected at random. (Source: The Hollywood Reporter)
a. Find the probability that both probable voters would like entertainers to address social and political issues.
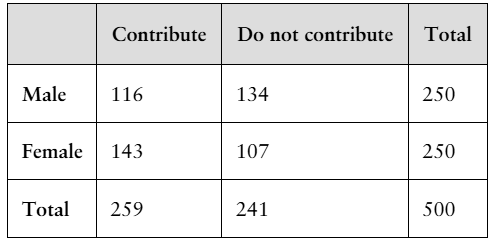
Problem 3.2.8a
"Finding Conditional Probabilities In Exercises 7 and 8, use the table to find each conditional probability.
8. Retirement Savings The table shows the results of a survey in which 250 male and 250 female workers ages 25 to 64 were asked if they contribute to a retirement savings plan at
work.
a. Find the probability that a randomly selected worker contributes to a retirement savings plan at work, given that the worker is male.
"
Problem 3.2.27a
"Using the Multiplication Rule In Exercises 19-32, use the Multiplication Rule.
27. Blood Types The probability that a person of Asian descent in the United States has type O+ blood is 39%. At random, six people of Asian descent in the United States are selected. (Source: American National Red Cross)
a. Find the probability that all six have type O+ blood."
Problem 3.2.39a
"39. Reliability of Testing A virus infects one in every 200 people. A test used to detect the virus in a person is positive 80% of the time when the person has the virus and 5% of the time when the person does not have the virus. (This 5% result is called a false positive.) Let A be the event ""the person is infected"" and B be the event ""the person tests positive.""
a. Using Bayes' Theorem, when a person tests positive, determine the probability that the person is infected."