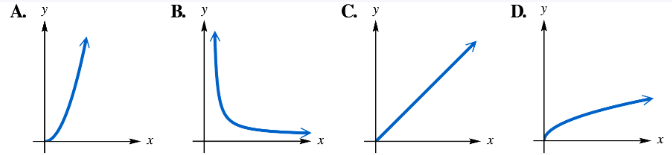
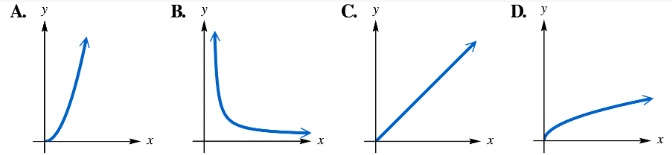
Match each statement with its corresponding graph in choices A–D. In each case, k > 0. y varies directly as x. (y=kx)

Use the factor theorem and synthetic division to determine whether the second polynomial is a factor of the first. x³+2x²+3; x-1

Solve each quadratic inequality. Give the solution set in interval notation. x² + x - 30 ≤ 0

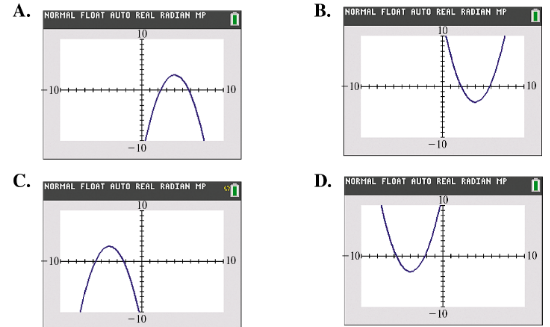
Match each function with its graph without actually entering it into a calculator. Then, after completing the exercises, check the answers with a calculator. Use the standard viewing window. ƒ(x) = (x + 4)² - 3

Use synthetic division to perform each division. $\frac{\frac{1}{3}{x}^3-\frac{2}{9}{x}^2+\frac{2}{27}x-\frac{1}{81}}{x-\frac{1}{3}}$

Graph each function. Determine the largest open intervals of the domain over which each function is (a) increasing or (b) decreasing. ƒ(x)=(1/3)(x+3)⁴-3

Use synthetic division to find ƒ(2). ƒ(x)=x⁵+4x²-2x-4

Use the factor theorem and synthetic division to determine whether the second polynomial is a factor of the first. 2x³+x+2; x+1

Graph each function. Determine the largest open intervals of the domain over which each function is (a) increasing or (b) decreasing. ƒ(x)=(1/2)(x-2)²+4

Match each statement with its corresponding graph in choices A–D. In each case, k > 0. y varies directly as the second power of x. (y=kx²)

Use the factor theorem and synthetic division to determine whether the second polynomial is a factor of the first. $2x^4+5x^3-2x^2+5x+6;x+3$

Graph the following on the same coordinate system.

(a) y = x²

(b) y = 3x²

(c) y = 1/3x²

(d) How does the coefficient of x² affect the shape of the graph?

Solve each quadratic inequality. Give the solution set in interval notation. x² - 2 > x

Use synthetic division to perform each division. (x⁴ - 3x³ - 4x² + 12x) / x-2

Use the factor theorem and synthetic division to determine whether the second polynomial is a factor of the first. See Example 1.

$5x^4+16x^3-15x^2+8x+16;x+4$

Write each formula as an English phrase using the word varies or proportional. C=2πr, where C is the circumference of a circle of radius r.

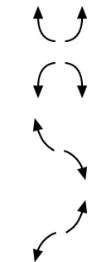
Use an end behavior diagram, as shown below, to describe the end behavior of the graph of each polynomial function. ƒ(x)=5x⁵+2x³-3x+4

Use synthetic division to perform each division. (x³ - 1) / (x-1)

Graph the following on the same coordinate system.

(a) y = (x - 2)²

(b) y = (x + 1)²

(c) y = (x + 3)²

(d) How do these graphs differ from the graph of y = x²?

If ƒ(x) is a polynomial function with real coefficients, and if 7+2i is a zero of the function, then what other complex number must also be a zero?

Solve each quadratic inequality. Give the solution set in interval notation. 2x² + 5 ≤ 11x

Use an end behavior diagram, as shown below, to describe the end behavior of the graph of each polynomial function. ƒ(x)=-x³-4x²+2x-1

Use synthetic division to perform each division. x⁴-1 / x-1

Factor ƒ(x) into linear factors given that k is a zero. $\text{ƒ}\left(x\right)=2x^3-3x^2-5x+6{;}^{}k=1$

Use one of the end behavior diagrams below, to describe the end behavior of the graph of each polynomial function.

$\text{ƒ}\left(x\right)=-4x^3+3x^2-1$

Write each formula as an English phrase using the word varies or proportional. r = d/t, where r is the speed when traveling d miles in t hours.

Graph each quadratic function. Give the (a) vertex, (b) axis, (c) domain, and (d) range. ƒ(x) = (x - 2)²

Solve each polynomial inequality. Give the solution set in interval notation.

(a) -x(x - 1)(x - 2) ≥ 0

(b) -x(x - 1)(x - 2) > 0

(c) -x(x - 1)(x - 2) ≤ 0

(d) -x(x - 1)(x - 2) < 0

Use synthetic division to perform each division. x⁷+1 / x+1

Use an end behavior diagram, as shown below, to describe the end behavior of the graph of each polynomial function. ƒ(x)=4x⁷-x⁵+x³-1