Provide a short answer to each question. What is the domain of the function ƒ(x)=1/x? What is its range?

Determine whether each statement is true or false. If false, explain why. Because x-1 is a factor of ƒ(x)=x⁶-x⁴+2x²-2, we can also conclude that ƒ(1) = 0.

Fill in the blank(s) to correctly complete each sentence. A polynomial function with leading term 3x⁵ has degree ____.

Provide a short answer to each question. What is the domain of the function $\text{ƒ}\left(x\right)=\frac{1}{x^2}$? What is its range?

Fill in the blank(s) to correctly complete each sentence. The highest point on the graph of a parabola that opens down is the ____ of the parabola.

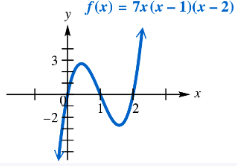
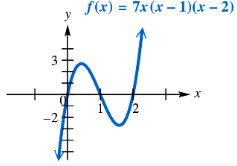
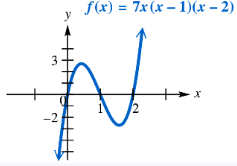
Use the graph to solve each equation or inequality. Use interval notation where appropriate. 7x(x - 1)(x - 2) = 0

Graph each quadratic function. Give the vertex, axis, x-intercepts, y-intercept, domain, range, and largest open intervals of the domain over which each function is increasing or decreasing. ƒ(x)=-3x²-12x-1

Fill in the blank(s) to correctly complete each sentence, or answer the question as appropriate. In the equation y = 6x, y varies directly as x. When x=5, y=30. What is the value of y when x=10?

Determine whether each statement is true or false. If false, explain why. For ƒ(x)=(x+2)⁴(x-3), the number 2 is a zero of multiplicity 4.

Use the graph to solve each equation or inequality. Use interval notation where appropriate. 7x(x - 1)(x - 2) < 0

Determine whether each statement is true or false. If false, explain why. A polynomial function having degree 6 and only real coefficients may have no real zeros.

Provide a short answer to each question. What is the equation of the vertical asymptote of the graph of y=[1/(x-3)]+2? Of the horizontal asymptote?

Using k as the constant of variation, write a variation equation for each situation. h varies inversely as t.

Use the graph to solve each equation or inequality. Use interval notation where appropriate. 7x(x - 1)(x - 2) > 0

Fill in the blank(s) to correctly complete each sentence. The vertex of the graph of ƒ(x) = x² + 2x + 4 has x-coordinate ____ .

Use the graph to solve each equation or inequality. Use interval notation where appropriate. 7x(x - 1)(x - 2) ≥ 0

Determine whether each statement is true or false. If false, explain why. The polynomial function $\text{ƒ}\left(x\right)=2x^5+3x^4-8x^3-5x+6$ has three variations in sign.

Solve each problem. If y varies directly as x, and y=20 when x=4, find y when x = -6.

Provide a short answer to each question. Is ƒ(x)=1/x² an even or an odd function? What symmetry does its graph exhibit?

Use synthetic division to perform each division. (x³ + 3x² +11x + 9) / x+1

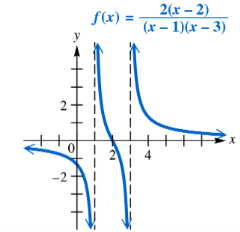
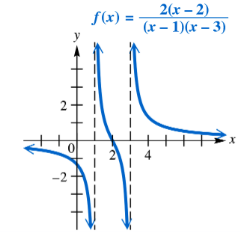
Use the graph to solve each equation or inequality. Use interval notation where appropriate. 2(x-2) / {(x-1)(x-3)} = 0

Solve each problem. During the course of a year, the number of volunteers available to run a food bank each month is modeled by $V\left(x\right)$, where $V\left(x\right)=2x^2-32x+150$ between the months of January and August. Here x is time in months, with x=1 representing January. From August to December, V(x) is modeled by $V\left(x\right)=31x-226$. Find the number of volunteers in each of the following months.

January

Solve each problem. During the course of a year, the number of volunteers available to run a food bank each month is modeled by $V\left(x\right)$, where $V\left(x\right)=2x^2-32x+150$ between the months of January and August. Here x is time in months, with x=1 representing January. From August to December, $V\left(x\right)$ is modeled by $V\left(x\right)=31x-226$. Find the number of volunteers in each of the following months.

May

Solve each problem. During the course of ayear, the number of volunteers available to run a food bank each month is modeled by $V\left(x\right),$ where $V\left(x\right)=2x^2-32x+150$ between the months of January and August. Here x is time in months, with x=1 representing January. From August to December, $V\left(x\right)$ is modeled by $V\left(x\right)=31x-226$. Find the number of volunteers in each of the following months.

August

Solve each problem. During the course of a year, the number of volunteers available to run a food bank each month is modeled by $V\left(x\right)$, where $V\left(x\right)=2x^2-32x+150$ between the months of January and August. Here x is time in months, with x=1 representing January. From August to December, $V\left(x\right)$ is modeled by $V\left(x\right)=31x-226$. Find the number of volunteers in each of the following months.

October

Solve each problem. During the course of a year, the number of volunteers available to run a food bank each month is modeled by $V\left(x\right)$, where $V\left(x\right)=2x^2-32x+150$ between the months of January and August. Here x is time in months, with x=1 representing January. From August to December, $V\left(x\right)$ is modeled by $V\left(x\right)=31x-226$. Find the number of volunteers in each of the following months.

December

Solve each problem. During the course of a year, the number of volunteers available to run a food bank each month is modeled by $V\left(x\right)$, where $V\left(x\right)=2x^2-32x+150$ between the months of January and August. Here x is time in months, with x=1 representing January. From August to December, $V\left(x\right)$ is modeled by $V\left(x\right)=31x-226$. Find the number of volunteers in each of the following months. Sketch a graph of $y=V\left(x\right)$ for January through December. In what month are the fewest volunteers available?

Determine whether each statement is true or false. If false, explain why. The product of a complex number and its conjugate is always a real number.

Use the graph to solve each equation or inequality. Use interval notation where appropriate. 2(x-2) / {(x-1)(x-3)} < 0

Provide a short answer to each question. Is ƒ(x)=1/x an even or an odd function? What symmetry does its graph exhibit?