Fill in the blank(s) to correctly complete each sentence. If ƒ(x) = 4^x, then ƒ(2) = and ƒ(-2) = ________.

Answer each of the following. Write log₃ 12 in terms of natural logarithms using the change-of-base theorem.

Fill in the blank(s) to correctly complete each sentence. The graph of ƒ(x) = -(1/3)^x+4-5 is that of ƒ(x) = (1/3)^x reflected across the ______ -axis, translated to the left ______ units and down _______ units.

Solve each equation. Round answers to the nearest hundredth as needed. (1/4)^x=64

Solve each equation. Round answers to the nearest hundredth as needed. x^2/3 =36

Answer each of the following. Between what two consecutive integers must log₂ 12 lie?

For ƒ(x) = 3^x and g(x)= (1/4)^x find each of the following. Round answers to the nearest thousandth as needed. See Example 1. ƒ(2)

If the statement is in exponential form, write it in an equivalent logarithmic form. If the statement is in logarithmic form, write it in exponential form. 3⁴ = 81

Solve each equation. In Exercises 11–34, give irrational solutions as decimals correct to the nearest thousandth. In Exercises 35-40, give solutions in exact form. 3^x = 7

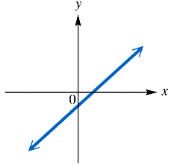
Determine whether each function graphed or defined is one-to-one.

Find each value. If applicable, give an approximation to four decimal places. log 10¹²

Solve each equation. In Exercises 11–34, give irrational solutions as decimals correct to the nearest thousandth. In Exercises 35-40, give solutions in exact form. (1/2)^x = 5

For ƒ(x) = 3^x and g(x)= (1/4)^x find each of the following. Round answers to the nearest thousandth as needed. ƒ(-2)

Find each value. If applicable, give an approximation to four decimal places. log 0.1

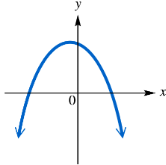
Determine whether each function graphed or defined is one-to-one.

Find each value. If applicable, give an approximation to four decimal places. log 63

Solve each equation. In Exercises 11–34, give irrational solutions as decimals correct to the nearest thousandth. In Exercises 35-40, give solutions in exact form. 0.8^x = 4

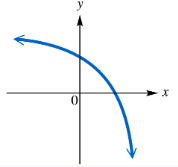
Determine whether each function graphed or defined is one-to-one.

For ƒ(x) = 3^x and g(x)= (1/4)^x find each of the following. Round answers to the nearest thousandth as needed. g(2)

For ƒ(x) = 3^x and g(x)= (1/4)^x find each of the following. Round answers to the nearest thousandth as needed. See Example 1. g(3)

If the statement is in exponential form, write it in an equivalent logarithmic form. If the statement is in logarithmic form, write it in exponential form. log₅ 5 = 1

Find each value. If applicable, give an approximation to four decimal places. log 0.0022

Determine whether each function graphed or defined is one-to-one. y = 2x - 8

If the statement is in exponential form, write it in an equivalent logarithmic form. If the statement is in logarithmic form, write it in exponential form. ${\log }_{\sqrt{3}}81=8$

Solve each equation. In Exercises 11–34, give irrational solutions as decimals correct to the nearest thousandth. In Exercises 35-40, give solutions in exact form. 4^(x-1) = 3^2x

For ƒ(x) = 3^x and g(x)= (1/4)^x find each of the following. Round answers to the nearest thousandth as needed. See Example 1. g(-3)

If the statement is in exponential form, write it in an equivalent logarithmic form. If the statement is in logarithmic form, write it in exponential form. log₄ 1/64 = -3

Find each value. If applicable, give an approximation to four decimal places. log(387 $\times$ 23)

Solve each equation. In Exercises 11–34, give irrational solutions as decimals correct to the nearest thousandth. In Exercises 35-40, give solutions in exact form. 6^(x+1) = 4^(2x-1)

Determine whether each function graphed or defined is one-to-one. y = -√(100 - x²)