Back
BackProblem 85
Graph each rational function. ƒ(x)=(20+6x-2x2)/(8+6x-2x2)
Problem 85
Use a graphing calculator to find the coordinates of the turning points of the graph of each polynomial function in the given domain interval. Give answers to the nearest hundredth. ƒ(x)=2x3-5x2-x+1; [1.4, 2]
Problem 85
Determine the different possibilities for the numbers of positive, negative, and nonreal complex zeros of each function.
Problem 86
Determine the different possibilities for the numbers of positive, negative, and nonreal complex zeros of each function.
Problem 86
A quadratic equation ƒ(x) = 0 has a solution x = 2. Its graph has vertex (5, 3). What is the other solution of the equation?
Problem 86
Solve each inequality. Give the solution set in interval notation. 4/(x+6)>2/(x-1)
Problem 86
Graph each rational function. ƒ(x)=(18+6x-4x2)/(4+6x+2x2)
Problem 87
Use a graphing calculator to find the coordinates of the turning points of the graph of each polynomial function in the given domain interval. Give answers to the nearest hundredth. ƒ(x)=x3+4x2-8x-8; [-3.8, -3]
Problem 87
Determine the different possibilities for the numbers of positive, negative, and nonreal complex zeros of each function.
Problem 88
Use a graphing calculator to find the coordinates of the turning points of the graph of each polynomial function in the given domain interval. Give answers to the nearest hundredth. ƒ(x)=x4-7x3+13x2+6x-28; [-1, 0]
Problem 88
Determine the different possibilities for the numbers of positive, negative, and nonreal complex zeros of each function.
Problem 89
Determine the different possibilities for the numbers of positive, negative, and nonreal complex zeros of each function.
Problem 90
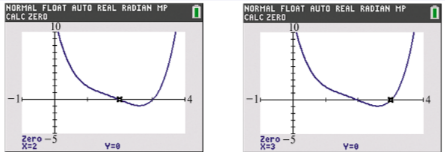
Solve each problem. A comprehensive graph of ƒ(x)=x4-7x3+18x2-22x+12 is shown in the two screens, along with displays of the two real zeros. Find the two remaining nonreal complex zeros.
Problem 90
Determine the different possibilities for the numbers of positive, negative, and nonreal complex zeros of each function. See Example 7. ƒ(x)=11x5-x3+7x-5
Problem 91
Use the technique described in Exercises 87–90 to solve each inequality. Write the solution set in interval notation. x2 - x - 6 < 0
Problem 91
Determine the different possibilities for the numbers of positive, negative, and nonreal complex zeros of each function.
Problem 92
Determine the different possibilities for the numbers of positive, negative, and nonreal complex zeros of each function. See Example 7. ƒ(x)=9x6-7x4+8x2+x+6
Problem 92
Use the technique described in Exercises 87–90 to solve each inequality. Write the solution set in interval notation. x2 - 9x + 20 < 0
Problem 93
Use the technique described in Exercises 87–90 to solve each inequality. Write the solution set in interval notation. 2x2 - 9x ≥ 18
Problem 93
Determine the different possibilities for the numbers of positive, negative, and nonreal complex zeros of each function.
Problem 93a
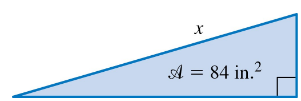
The following exercises are geometric in nature and lead to polynomial models. Solve each problem. A certain right triangle has area 84 in.2. One leg of the triangle measures 1 in. less than the hypotenuse. Let x represent the length of the hypotenuse. Express the length of the leg mentioned above in terms of x. Give the domain of x.
Problem 94
Use the technique described in Exercises 87–90 to solve each inequality. Write the solution set in interval notation. 3x2 + x ≥ 4
Problem 94
Determine the different possibilities for the numbers of positive, negative, and nonreal complex zeros of each function.
Problem 95
Use the technique described in Exercises 87–90 to solve each inequality. Write the solution set in interval notation. -x2 + 4x + 1 ≥ 0
Problem 95
Find all complex zeros of each polynomial function. Give exact values. List multiple zeros as necessary.* ƒ(x)=x4+2x3-3x2+24x-180
Problem 96
Use the technique described in Exercises 87–90 to solve each inequality. Write the solution set in interval notation. -x2 + 2x + 6 > 0
Problem 96a
The following exercises are geometric in nature and lead to polynomial models. Solve each problem. A standard piece of notebook paper measuring 8.5 in. by 11 in. is to be made into a box with an open top by cutting equal-size squares from each cor-ner and folding up the sides. Let x represent the length of a side of each such square in inches. Use the table feature of a graphing calculator to do the following. Round to the nearest hundredth.
a. Find the maximum volume of the box.
Problem 96b
The following exercises are geometric in nature and lead to polynomial models. Solve each problem. A standard piece of notebook paper measuring 8.5 in. by 11 in. is to be made into a box with an open top by cutting equal-size squares from each corner and folding up the sides. Let x represent the length of a side of each such square in inches. Use the table feature of a graphing calculator to do the following. Round to the nearest hundredth.
b. Determine when the volume of the box will be greater than 40 in.3.
Problem 97
Find all complex zeros of each polynomial function. Give exact values. List multiple zeros as necessary.
Problem 99
Find all complex zeros of each polynomial function. Give exact values. List multiple zeros as necessary.