Graph each rational function. See Examples 5–9.

$\text{ƒ}\left(x\right)=\left[\right(x+6\left)\right(x-2\left)\right]/\left[\right(x+3\left)\right(x-4\left)\right]$

Graph each rational function. ƒ(x)=[(x+3)(x-5)]/[(x+1)(x-4)]

Height of an Object If an object is projected upward from an initial height of 100 ft with an initial velocity of 64 ft per sec, then its height in feet after t seconds is given by $s\left(t\right)=-16t^2+64t+100$. Find the number of seconds it will take the object to reach its maximum height. What is this maximum height?

Find a polynomial function ƒ(x) of least degree having only real coefficients and zeros as given. Assume multiplicity 1 unless otherwise stated. 2-i and 6-3i

Graph each rational function. ƒ(x)=(3x²+3x-6)/(x²-x-12)

Solve each problem. Work each of the following. Sketch the graph of a function that does not intersect its horizontal asymptote y=1, has the line x=3 as a vertical asymptote, and has x-intercepts (2, 0) and (4, 0).

Solve each problem. Work each of the following. Find an equation for a possible corresponding rational function.

Solve each problem. Work each of the following. Find an equation for a possible corresponding rational function.

Graph each rational function. ƒ(x)=(9x²-1)/(x²-4)

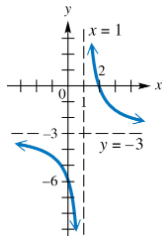
Solve each problem. Find a rational function ƒ having the graph shown.

Graph each rational function. See Examples 5–9.

$\text{ƒ}\left(x\right)=(16x^2-9)/(x^2-9)$

Solve each problem. This rational function has two holes and one vertical asymptote.

$\text{ƒ}\left(x\right)=\frac{(x^3+7x^2-25x-175)}{(x^3+3x^2-25x-75)}$

What are the x-values of the holes?

Solve each inequality. Give the solution set in interval notation. (2x-1)(x+5)<0

Determine the different possibilities for the numbers of positive, negative, and nonreal complex zeros of each function. $\text{ƒ}\left(x\right)=2x^3-4x^2+2x+7$

Determine the different possibilities for the numbers of positive, negative, and nonreal complex zeros of each function. See Example 7. ƒ(x)=x³+2x²+x-10

Determine the different possibilities for the numbers of positive, negative, and nonreal complex zeros of each function. $\text{ƒ}\left(x\right)=4x^3-x^2+2x-7$

Solve each inequality. Give the solution set in interval notation. (x-4)(x-1)(x+2)>0

Find a value of c so that y = x² - 10x + c has exactly one x-intercept.

For what values of a does y = ax² - 8x + 4 have no x-intercepts?

Determine the different possibilities for the numbers of positive, negative, and nonreal complex zeros of each function. $\text{ƒ}\left(x\right)=3x^3+6x^2+x+7$

Graph each rational function. ƒ(x)=[(x-5)(x-2)]/(x²+9)

Define the quadratic function ƒ having x-intercepts (2, 0) and (5, 0) and y-intercept (0, 5).

Use a graphing calculator to find the coordinates of the turning points of the graph of each polynomial function in the given domain interval. Give answers to the nearest hundredth. ƒ(x)=2x³-5x²-x+1; [-1, 0]

Graph each rational function. ƒ(x)=(x²+8x+16)/(x²+4x-5)

Determine the different possibilities for the numbers of positive, negative, and nonreal complex zeros of each function. $\text{ƒ}\left(x\right)=5x^4+3x^2+2x-9$

Graph each rational function. ƒ(x)=(x²+2x+1)/(x²-x-6)

Solve each inequality. Give the solution set in interval notation. (x+7)/(2x+1)<0

Define the quadratic function ƒ having x-intercepts (1, 0) and (-2, 0) and y-intercept (0, 4).

Determine the different possibilities for the numbers of positive, negative, and nonreal complex zeros of each function. $\text{ƒ}\left(x\right)=3x^4+2x^3-8x^2-10x-1$

The distance between the two points $P(x_1,y_1)$ and $R(x_2,y_2)$ is $d(P, R) = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2}$. Distance formula. Find the closest point on the line $y=2x$ to the point $(1,7)$. (Hint: Every point on $y=2x$ has the form $(x,2x)$, and the closest point has the minimum distance.)