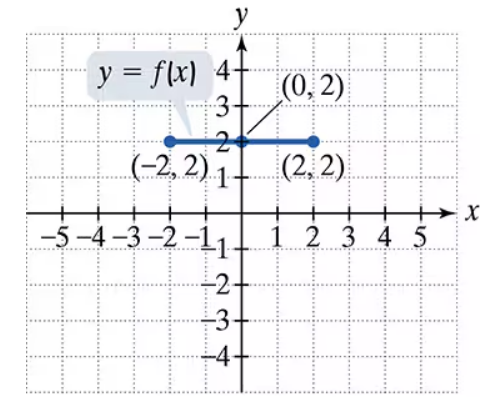
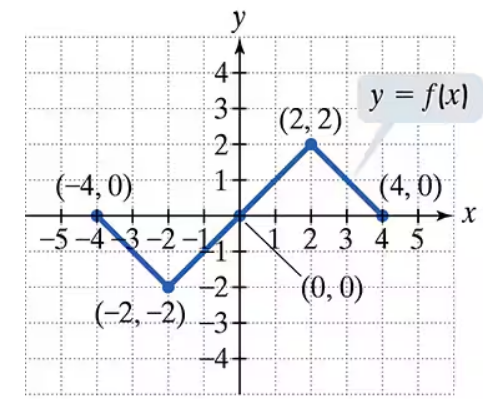
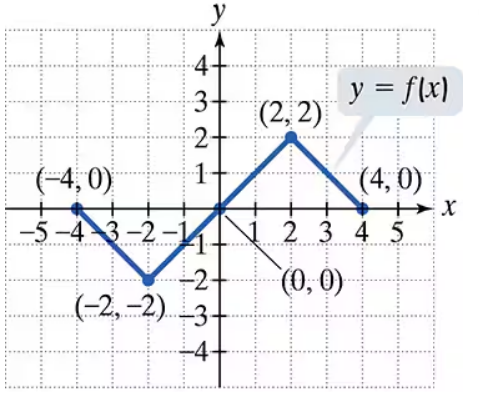
Use the graph of y = f(x) to graph each function g.

g(x) = −ƒ( x/2) +1

Find the distance between each pair of points. If necessary, express answers in simplified radical form and then round to two decimal places. (3√3, √5) and (−√3, 4√5)

The functions in Exercises 11-28 are all one-to-one. For each function, a. Find an equation for f^-1(x), the inverse function. b. Verify that your equation is correct by showing that f(ƒ^-1 (x)) = = x and ƒ^-1 (f(x)) = x. f(x) = 2x + 3

Use the vertical line test to identify graphs in which y is a function of x.

Find the average rate of change of the function from x₁ to x₂. f(x) = x² + 2x from x₁ = 3 to x₂ = 5

Find the domain of each function. f(x) = 1/[4/(x - 1) - 2]

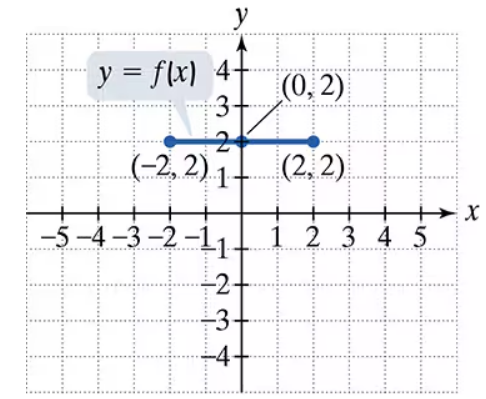
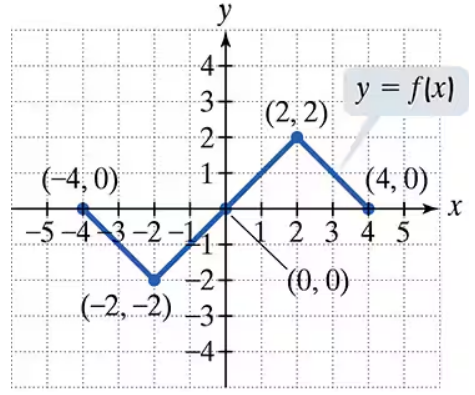
In Exercises 1-16, use the graph of y = f(x) to graph each function g.

g(x) = -f(2x) - 1

Use the given conditions to write an equation for each line in point-slope form and slope-intercept form. Slope = -5, passing through (-4, -2)

Use the graph of y = f(x) to graph each function g.

g(x) = f(x) - 1

The functions in Exercises 11-28 are all one-to-one. For each function, a. Find an equation for f^-1(x), the inverse function. b. Verify that your equation is correct by showing that f(ƒ^-1 (x)) = = x and ƒ^-1 (f(x)) = x. f(x) = x³ +2

Find the distance between each pair of points. If necessary, express answers in simplified radical form and then round to two decimal places. (7/3, 1/5) and (1/3, 6/5)

Find the average rate of change of the function from x₁ to x₂. f(x) = √x from x₁ = 4 to x₂ = 9

In Exercises 11–26, determine whether each equation defines y as a function of x. x = y²

Find the domain of each function. f(x) = √(x - 3)

Find the distance between each pair of points. If necessary, express answers in simplified radical form and then round to two decimal places. (-1/4, -1/7) and (3/4, 6/7)

Use the graph to determine (a) the function's domain, (b) the function's range, (c) the x-intercepts, if any, (d) the y-intercept, if there is one, (e) intervals on which the function is increasing, decreasing or constant, (f) the missing function values, indicated by question marks, below each graph.

In Exercises 11–26, determine whether each equation defines y as a function of x. 4x = y²

Find the domain of each function. f(x) = 1/√(x - 3)

use the graph of y = f(x) to graph each function g.

g(x) = f(x-1)

Find the midpoint of each line segment with the given endpoints. (6, 8) and (2, 4)

Write an equation in slope-intercept form of a linear function f whose graph satisfies the given conditions. The graph of ƒ passes through (−1, 5) and is perpendicular to the line whose equation is x = 6.

The functions in Exercises 11-28 are all one-to-one. For each function, a. Find an equation for f^-1(x), the inverse function. b. Verify that your equation is correct by showing that f(ƒ^-1 (x)) = = x and ƒ^-1 (f(x)) = x. f(x) = (x+2)³

Determine whether each equation defines y as a function of x. y = √x +4

Write an equation in slope-intercept form of a linear function f whose graph satisfies the given conditions. The graph of ƒ passes through (−2, 6) and is perpendicular to the line whose equation is x = -4.

Use the graph of y = f(x) to graph each function g. g(x) = f(x+1)

Determine whether each equation defines y as a function of x. $y=-\sqrt{x+4}$

Use the given conditions to write an equation for each line in point-slope form and slope-intercept form. Slope = −1, passing through (−4, − 1/4)

Write an equation in slope-intercept form of a linear function f whose graph satisfies the given conditions. The graph of ƒ passes through (−6, 4) and is perpendicular to the line that has an x intercept of 2 and a y-intercept of -4.

Find the midpoint of each line segment with the given endpoints. (-2, -8) and (−6, −2)

Find the domain of each function. f(x) = √(5x+35)