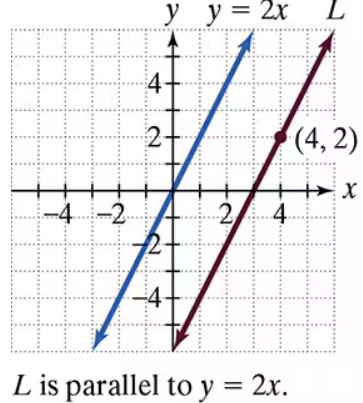
Write an equation for line L in point-slope form and slope-intercept form.

Find the slope of the line passing through each pair of points or state that the slope is undefined. Then indicate whether the line through the points rises, falls, is horizontal, or is vertical. (4, 7) and (8, 10)

Find f(g(x)) and g (f(x)) and determine whether each pair of functions ƒ and g are inverses of each other. f(x) = 4x and g(x) = x/4

Find the domain of each function. f(x)=3(x-4)

Find the distance between each pair of points. If necessary, express answers in simplified radical form and then round to two decimal places. (2, 3) and (14, 8)

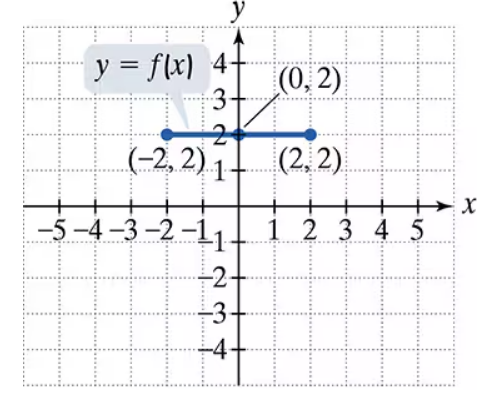
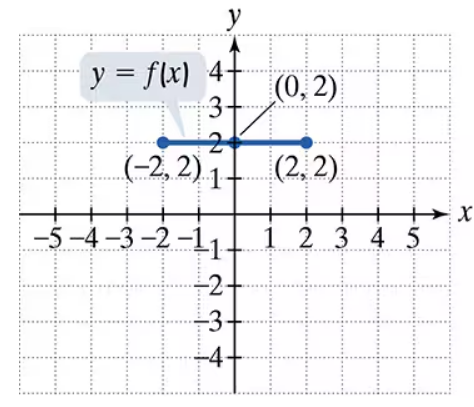
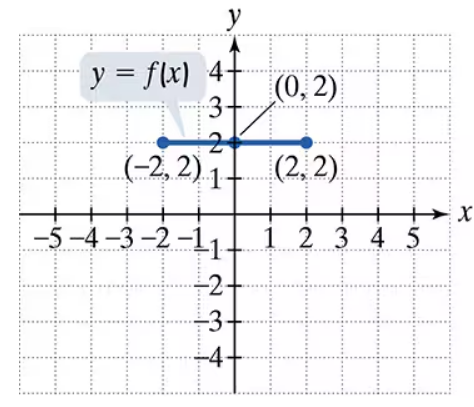
Use the graph of y = f(x) to graph each function g.

g(x) = f(x)+1

Determine whether each relation is a function. Give the domain and range for each relation.{(1, 2), (3, 4), (5, 5)}

Determine whether each relation is a funciton, Give the domain and range for each relation. (1, 10), (2, 500), (13, π)

Find the domain of each function. f(x) = 2(x+5)

Find the distance between each pair of points. If necessary, express answers in simplified radical form and then round to two decimal places. (4, -1) and (-6, 3)

Find the domain of each function. g(x) = 3/(x-4)

Find the slope of the line passing through each pair of points or state that the slope is undefined. Then indicate whether the line through the points rises, falls, is horizontal, or is vertical. (-2, 1) and (2, 2)

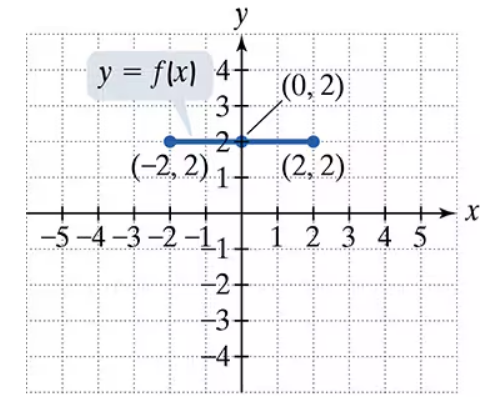
Use the graph of y = f(x) to graph each function g.

g(x) = f(x+1)

Write an equation for line L in point-slope form and slope-intercept form.

Find f(g(x)) and g (f(x)) and determine whether each pair of functions ƒ and g are inverses of each other. f(x)=3x+8 and g(x) = (x-8)/3

Determine whether each relation is a function. Give the domain and range for each relation. {(3, 4), (3, 5), (4, 4), (4, 5)}

Determine whether each equation defines y as a function of x. 2x + y = 8

Find f(g(x)) and g (f(x)) and determine whether each pair of functions ƒ and g are inverses of each other. f(x) = 4x + 9 and g(x) = (x-9)/4

Find the domain of each function. g(x) = 2/(x+5)

Find the domain of each function. f(x) = x² - 2x - 15

Find f(g(x)) and g (f(x)) and determine whether each pair of functions ƒ and g are inverses of each other. f(x)=5x-9 and g(x) = (x+5)/9

Use the given conditions to write an equation for each line in point-slope form and slope-intercept form. Passing through (−8, −10) and parallel to the line whose equation is y = −4x + 3

Use the graph of y = f(x) to graph each function g.

g(x) = f(x-1) - 2

In Exercises 1–10, determine whether each relation is a function. Give the domain and range for each relation. {(3, −2), (5, −2), (7, 1), (4, 9)}

Determine whether each equation defines y as a function of x. 2x + y^2 = 6

Find the distance between each pair of points. If necessary, express answers in simplified radical form and then round to two decimal places. (0, 0) and (3,-4)

Find the slope of the line passing through each pair of points or state that the slope is undefined. Then indicate whether the line through the points rises, falls, is horizontal, or is vertical. (4, -1) and (3, −1)

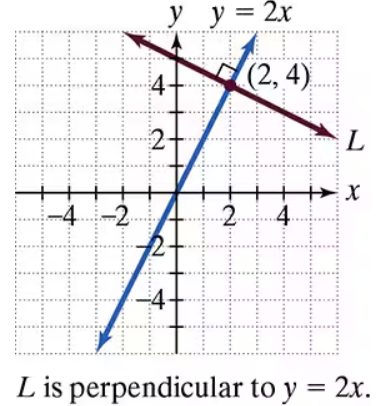
Use the given conditions to write an equation for each line in point-slope form and slope-intercept form. Passing through (2, −3) and perpendicular to the line whose equation is y = (1/5)x + 6

In Exercises 1–10, determine whether each relation is a function. Give the domain and range for each relation. {(-3, -3), (-2, −2), (−1, −1), (0, 0)}

Use the graph of y = f(x) to graph each function g.

g(x) = f(-x)