 Back
BackProblem 1
Solve each equation in Exercises 1 - 14 by factoring.
Problem 1
In Exercises 1–14, express each interval in set-builder notation and graph the interval on a number line. (1, 6]
Problem 1
Graph each equation in Exercises 1–4. Let x= -3, -2. -1, 0, 1, 2 and 3. y = 2x-2
Problem 1
Solve and check each linear equation. 4x + 9 = 33
Problem 1
In Exercises 1–8, add or subtract as indicated and write the result in standard form. (7 + 2i) + (1 - 4i)
Problem 1a
Plot the given point in a rectangular coordinate system. (1, 4)
Problem 2
Graph each equation in Exercises 1–4. Let x= -3, -2. -1, 0, 1, 2 and 3. y = x^2-3
Problem 2
Solve each polynomial equation in Exercises 1–10 by factoring and then using the zero-product principle.
Problem 3
In Exercises 1–26, solve and check each linear equation. 7x - 5 = 72
Problem 3
In Exercises 1–8, add or subtract as indicated and write the result in standard form. (3 + 2i) - (5 - 7i)
Problem 3
In Exercises 1–14, express each interval in set-builder notation and graph the interval on a number line. [- 5, 2)
Problem 3
Solve each equation in Exercises 1 - 14 by factoring.
Problem 3a
Plot the given point in a rectangular coordinate system. (- 2, 3)
Problem 4
Graph each equation in Exercises 1–4. Let x= -3, -2. -1, 0, 1, 2 and 3. y = |x|-2
Problem 4
Solve each polynomial equation in Exercises 1–10 by factoring and then using the zero-product principle.
Problem 5
Solve each equation in Exercises 1 - 14 by factoring.
Problem 5
In Exercises 1–14, express each interval in set-builder notation and graph the interval on a number line. [- 3, 1]
Problem 5
In Exercises 1–8, add or subtract as indicated and write the result in standard form. 6 - (- 5 + 4i) - (- 13 - i)
Problem 5a
Solve and check each linear equation. 3(x - 1) = 21
Problem 6
In Exercises 6–8, use the graph and determine the x-intercepts if any, and the y-intercepts if any. For each graph, tick marks along the axes represent one unit each.

Problem 6a
Plot the given point in a rectangular coordinate system. (- 4, - 2)
Problem 7
Solve each equation in Exercises 1 - 14 by factoring.
Problem 7
A new car worth $36,000 is depreciating in value by $4000 per year. a. Write a formula that models the car's value, y, in dollars, after x years. b. Use the formula from part (a) to determine after how many years the car's value will be $12,000. c. Graph the formula from part (a) in the first quadrant of a rectangular coordinate system. Then show your solution to part (b) on the graph.
Problem 7
Solve each polynomial equation in Exercises 1–10 by factoring and then using the zero-product principle.
Problem 7
In Exercises 1–14, express each interval in set-builder notation and graph the interval on a number line. (2, ∞)
Problem 7
In Exercises 1–8, add or subtract as indicated and write the result in standard form. 8i - (14 - 9i)
Problem 7
In Exercises 6–8, use the graph and determine the x-intercepts if any, and the y-intercepts if any. For each graph, tick marks along the axes represent one unit each.
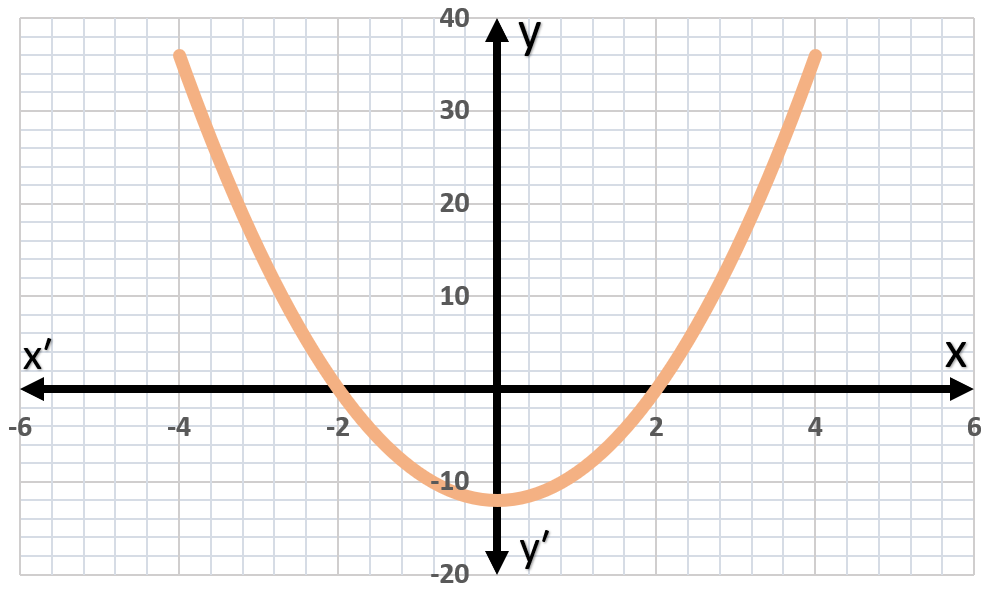
Problem 7a
Solve and check each linear equation. 11x - (6x - 5) = 40
Problem 8
A new car worth $45,000 is depreciating in value by $5000 per year. a. Write a formula that models the car's value, y, in dollars, after x years. b. Use the formula from part (a) to determine after how many years the car's value will be $10,000. c. Graph the formula from part (a) in the first quadrant of a rectangular coordinate system. Then show your solution to part (b) on the graph.
Problem 9
Solve each equation in Exercises 1 - 14 by factoring.
