In Exercises 1–10, determine whether each relation is a function. Give the domain and range for each relation. {(-3, -3), (-2, −2), (−1, −1), (0, 0)}

Use the given conditions to write an equation for each line in point-slope form and slope-intercept form. Passing through (2, −3) and perpendicular to the line whose equation is y = (1/5)x + 6

Find the domain of each function. g(x) = 3/(x²-2x-15)

Evaluate each function at the given values of the independent variable and simplify. g(x) = 3x^2 - 5x + 2 (a) g(0), (b) g(-2), (c) g(x-1), (d) g(-x)

Use the given conditions to write an equation for each line in point-slope form and general form. Passing through (−2, 2) and parallel to the line whose equation is 2x-3y-7=0

In Exercises 1–10, determine whether each relation is a function. Give the domain and range for each relation. {(1, 4), (1, 5), (1, 6)}

Find f(g(x)) and g (f(x)) and determine whether each pair of functions ƒ and g are inverses of each other. f(x) = = -x and g(x) = -x

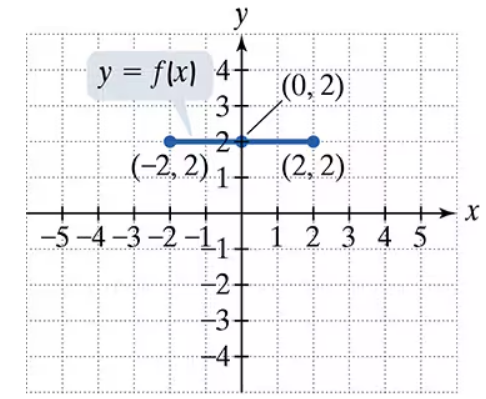
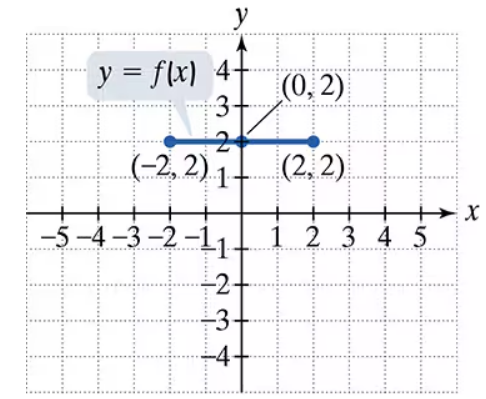
Use the graph of y = f(x) to graph each function g.

g(x) = -f(x) +3

Find the domain of each function. f(x) = 1/(x+7) + 3/(x-9)

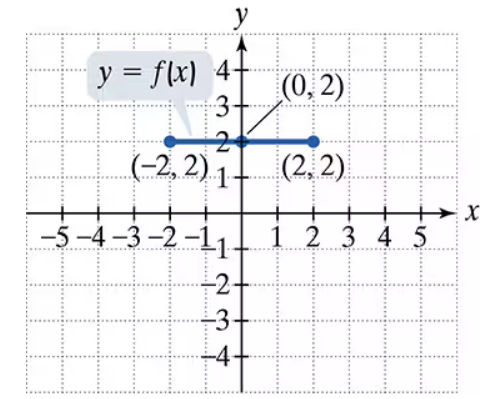
Use the graph of y = f(x) to graph each function g.

g(x) = f(-x)+3

Find f(g(x)) and g (f(x)) and determine whether each pair of functions ƒ and g are inverses of each other. f(x) = ∛(x − 4) and g(x) = x³ +4

Evaluate each function at the given values of the independent variable and simplify. (a) f(-2), (b) f(1), (c) f(2)

Use the given conditions to write an equation for each line in point-slope form and general form. Passing through (4, −7) and perpendicular to the line whose equation is x − 2y – 3 = 0

The functions in Exercises 11-28 are all one-to-one. For each function, a. Find an equation for f^-1(x), the inverse function. b. Verify that your equation is correct by showing that f(ƒ^-1 (x)) = = x and ƒ^-1 (f(x)) = x. f(x) = x +3

Find the distance between each pair of points. If necessary, express answers in simplified radical form and then round to two decimal places. (3.5, 8.2) and (-0.5, 6.2)

In Exercises 11–26, determine whether each equation defines y as a function of x. x + y = 16

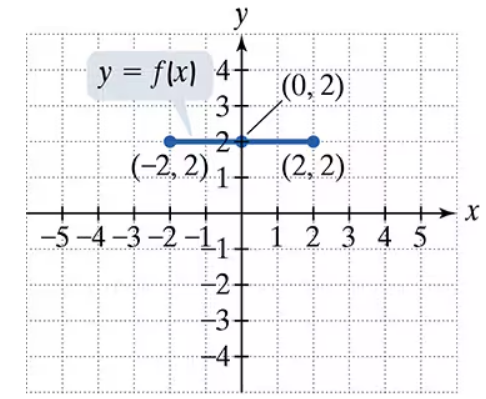
Use the graph of y = f(x) to graph each function g.

g(x) = ½ f(x)

Use the given conditions to write an equation for each line in point-slope form and slope-intercept form. Slope = 2, passing through (3, 5)

Find the domain of each function. f(x) = 1/(x²+1) - 1/(x²-1)

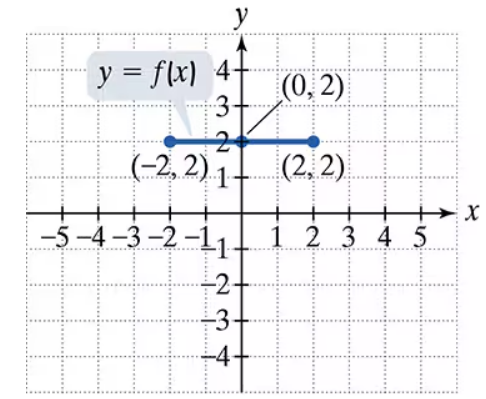
Use the graph of y = f(x) to graph each function g.

g(x) = 2f(x)

Use the vertical line test to identify graphs in which y is a function of x.

Use the given conditions to write an equation for each line in point-slope form and general form. Passing through (5, −9) and perpendicular to the line whose equation is x + 7y - 12= 0

Find the distance between each pair of points. If necessary, express answers in simplified radical form and then round to two decimal places. (0, −√3) and (√5, 0)

The functions in Exercises 11-28 are all one-to-one. For each function, a. Find an equation for f^-1(x), the inverse function. b. Verify that your equation is correct by showing that f(ƒ^-1 (x)) = = x and ƒ^-1 (f(x)) = x. f(x) = 2x

Find the average rate of change of the function from x₁ to x₂. f(x) = 3x from x₁ = 0 to x₂ = 5

Use the graph of y = f(x) to graph each function g.

g(x) = f(x/2)

Find the domain of each function. h(x) = 4/(3/x - 1)

In Exercises 11–26, determine whether each equation defines y as a function of x. x² + y = 25

Find the distance between each pair of points. If necessary, express answers in simplified radical form and then round to two decimal places. (0, -√2) and (√7,0)

Use the given conditions to write an equation for each line in point-slope form and slope-intercept form. Slope = 8, passing through (4, −1)