Back
BackProblem 9.3.10
"In Exercises 7-10, use the value of the correlation coefficient r to calculate the coefficient of determination r^2. What does this tell you about the explained variation of the data about the regression line? about the unexplained variation?
10. r =0.881"
Problem 9.3.33
"Old Vehicles In Exercises 31–34, use the figure shown at the left.
33. Coefficient of Determination Find the coefficient of determination r^2 and interpret the results."
Problem 9.3.21
"Constructing and Interpreting a Prediction Interval In Exercises 21-30, construct the indicated prediction interval and interpret the results.
21. Proceeds Construct a 95% prediction interval for the proceeds from initial public offerings in Exercise 11 when the number of offerings is 200."
Problem 9.3.22
"Constructing and Interpreting a Prediction Interval In Exercises 21-30, construct the indicated prediction interval and interpret the results.
22. Mean Hourly Wage Construct a 95% prediction interval for the mean hourly wage in Exercise 12 when the median hourly wage is $21.50."
Problem 9.3.31
"Old Vehicles In Exercises 31–34, use the figure shown at the left.
Scatter Plot Construct a scatter plot of the data. Show y and x on the graph."
Problem 9.3.32
"Old Vehicles In Exercises 31–34, use the figure shown at the left.
Regression Line Find and draw the regression line."
Problem 9.3.34
"Old Vehicles In Exercises 31–34, use the figure shown at the left.
Error of Estimate Find the standard error of estimate Se and interpret the results."
Problem 9.3.23
"Constructing and Interpreting a Prediction Interval In Exercises 21-30, construct the indicated prediction interval and interpret the results.
23. Points Earned Construct a 90% prediction interval for total points earned in Exercise 13 when the number of goals allowed by the team is 140."
Problem 9.3.24
"Constructing and Interpreting a Prediction Interval In Exercises 21-30, construct the indicated prediction interval and interpret the results.
24. Trees Construct a 90% prediction interval for the trunk diameter of a tree in Exercise 14 when the height is 80 feet."
Problem 9.3.25
"Constructing and Interpreting a Prediction Interval In Exercises 21-30, construct the indicated prediction interval and interpret the results.
25. Mean Wage Construct a 99% prediction interval for the mean annual wage in Exercise 15 when the percentage of employment in STEM occupations is 13% in the industry."
Problem 9.3.26
"Constructing and Interpreting a Prediction Interval In Exercises 21-30, construct the indicated prediction interval and interpret the results.
26. Voter Turnout Construct a 99% prediction interval for number of ballots cast in Exercise 16 when the voting age population is 210 million."
Problem 9.3.27
"Constructing and Interpreting a Prediction Interval In Exercises 21-30, construct the indicated prediction interval and interpret the results.
27. Natural Gas Construct a 95% prediction interval for the export of natural gas from the United States in Exercise 17 when the marketed production of natural gas in the United States is 31 trillion cubic feet."
Problem 9.3.28
"Constructing and Interpreting a Prediction Interval In Exercises 21-30, construct the indicated prediction interval and interpret the results.
28. Total Assets Construct a 90% prediction interval for the total assets in federal defined benefit plans in Exercise 18 when the total assets in IRAs are $6400 billion."
Problem 9.3.29
"Constructing and Interpreting a Prediction Interval In Exercises 21-30, construct the indicated prediction interval and interpret the results.
29. New Vehicle Sales Construct a 95% prediction interval for new vehicle sales for General Motors in Exercise 19 when the number of new vehicles sold by Ford is 2028 thousand."
Problem 9.3.30
"Constructing and Interpreting a Prediction Interval In Exercises 21-30, construct the indicated prediction interval and interpret the results.
30. New Vehicle Sales Construct a 99% prediction interval for new vehicle sales for Honda in Exercise 20 when the number of new vehicles sold by Toyota is 2159 thousand."
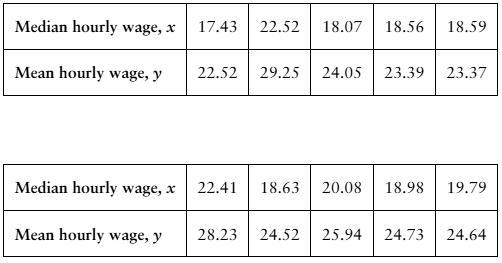
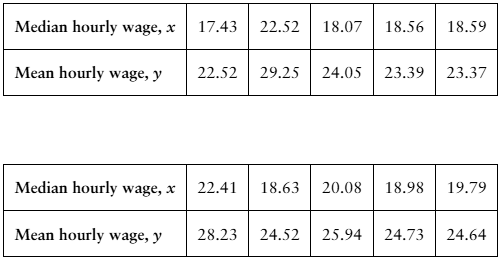
Problem 9.3.12a
"Finding the Coefficient of Determination and the Standard Error of Estimate In Exercises 11-20, use the data to (a) find the coefficient of determination r^2 and interpret the result,
12. [APPLET] Median and Mean Hourly Wages The table shows the median and mean hourly wages (in dollars) in 10 states in a recent year. The equation of the regression line is y = 1.208x + 1.495. (Source: U.S. Census Bureau)
"
Problem 9.3.12b
"Finding the Coefficient of Determination and the Standard Error of Estimate In Exercises 11-20, use the data to (b) find the standard error of estimate s_e and interpret the result.
12. [APPLET] Median and Mean Hourly Wages The table shows the median and mean hourly wages (in dollars) in 10 states in a recent year. The equation of the regression line is y = 1.208x + 1.495. (Source: U.S. Census Bureau)
"
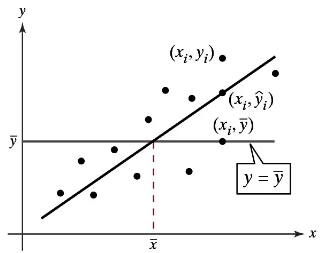
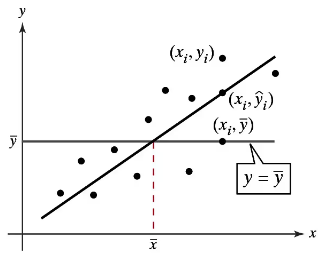
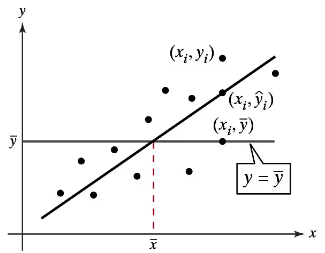
Problem 9.3.1
"Graphical Analysis In Exercises 1–3, use the figure.
1. Describe the total variation about a regression line in words and in symbols."
Problem 9.3.2
"Graphical Analysis In Exercises 1–3, use the figure.
2. Describe the explained variation about a regression line in words and in symbols."
Problem 9.3.3
"Graphical Analysis In Exercises 1–3, use the figure.
Describe the unexplained variation about a regression line in words and in symbols."
Problem 9.3.38
"Confidence Intervals for y-Intercept and Slope
You can construct confidence intervals for the y-intercept B and slope M of the regression line y = Mx + B for the population by using the inequalities below.
y-intercept B :
b - E < B < b + E
where
E = t_c s_e \sqrt{\frac{1}{n} + \frac{\overline{x}^2}{\sum x^2 - \frac{(\Sigma x)^2}{n}}}
slope M :
m - E < M < m + E
where
E = \frac{t_c s_e}{\sqrt{\sum x^2 - \frac{(\Sigma x)^2}{n}}}
The values of m and b are obtained from the sample data, and the critical value t_c is found using Table 5 in Appendix B with n - 2 degrees of freedom.
In Exercises 37 and 38, construct the indicated confidence intervals for B and M using the gross domestic products and carbon dioxide emissions data found in Example 2.
38. 99% confidence interval"
Problem 9.4.1
1. Interpret the meaning of the coefficient -8.2 in the multiple regression equation y=112.1+0.43x_1-8.2x_2+29.5x_3.
Problem 9.4.2
2. Compare the numbers of dependent and independent variables in a multiple regression equation and a single regression equation.
Problem 9.4.3
"Predicting y-Values In Exercises 3-6, use the multiple regression equation to predict the y-values for the values of the independent variables.
3. Cauliflower Yield The equation used to predict the annual cauliflower yield (in pounds
per acre) is y=24,791+4.508x_1-4.723x_2
where x_1 is the number of acres planted and x_2 is the number of acres harvested.(Adapted from United States Department of Agriculture)
a. x_1 = 36,500, x_2 = 36,100
b. x_1 = 38,100, x_2 = 37,800
c. x_1 = 39,000, x_2 = 38,800
d. x_1 = 42,200, x_2 = 42,100"
Problem 9.4.4
"Predicting y-Values In Exercises 3-6, use the multiple regression equation to predict the y-values for the values of the independent variables.
4. Sorghum Yield The equation used to predict the annual sorghum yield (in bushels per
acre) is y = 80.1-20.2x_1 +21.2x_2
where x_1 is the number of acres planted (in millions) and x_2 is the number of acres harvested (in millions). (Adapted from United States Department of Agriculture)
a. x_1 = 5.5, x_2 = 3.9
b. x_1 = 8.3, x_2 = 7.3
c. x_1 = 6.5, x_2 = 5.7
d. x_1 = 9.4, x_2= 7.8"
Problem 9.4.6
"Predicting y-Values In Exercises 3-6, use the multiple regression equation to predict the y-values for the values of the independent variables.
6. Elephant Weight The equation used to predict the weight of an elephant (in kilograms) is
y =- 4016+11.5x_1+7.55x_2+12.5x_3
where x_1 represents the girth of the elephant (in centimeters), x_2 represents the length of the elephant (in centimeters), and x_3 represents the circumference of a footpad (in
centimeters). (Source: Field Trip Earth)
a. x_1 = 421, x_2 = 224, x_3 = 144
b. x_1 = 311, x_2 = 171, x_3 = 102
c. x_1 = 376, x_2 = 226, x_3 = 124
d. x_1 =231, x_2 = 135, x_3 = 86"
Problem 9.4.5
"Predicting y-Values In Exercises 3-6, use the multiple regression equation to predict the y-values for the values of the independent variables.
5. Black Cherry Tree Volume The volume (in cubic feet) of a black cherry tree can be modeled by the equation
y =- 52.2+0.3x_1 +4.5x_2
where x_1 is the tree's height (in feet) and x_2 is the tree's diameter (in inches). (Source: Journal of the Royal Statistical Society)
a. x_1 = 70, x_2 = 8.6
b. x_1 = 65, x_2 = 11.0
c. x_1 = 83, x_2 = 17.6
d. x_1 = 87, x_2 = 19.6"