Here are the essential concepts you must grasp in order to answer the question correctly.
Runs Test
The Runs Test is a non-parametric statistical test used to determine the randomness of a sequence of data. It analyzes the occurrence of 'runs,' which are sequences of consecutive identical elements, to assess whether the observed pattern deviates from what would be expected in a random sequence. This test is particularly useful in quality control and in analyzing time series data.
Recommended video:
Step 2: Calculate Test Statistic
Significance Level
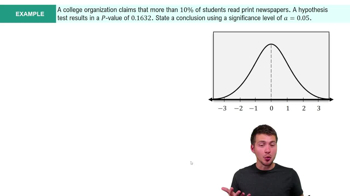
The significance level, often denoted as alpha (α), is the threshold used to determine whether to reject the null hypothesis in hypothesis testing. A common significance level is 0.05, which indicates a 5% risk of concluding that a difference exists when there is no actual difference. In the context of the Runs Test, it helps to establish the critical values that define the boundaries for accepting or rejecting the hypothesis of randomness.
Recommended video:
Step 4: State Conclusion Example 4
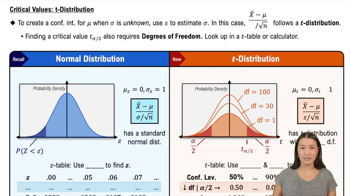
Critical Values
Critical values are the points in a statistical distribution that define the boundaries for rejecting the null hypothesis. In the context of the Runs Test, these values are derived from statistical tables and are used to compare against the calculated number of runs from the data. If the number of runs falls outside the critical values, it suggests that the sequence is not random, leading to a rejection of the null hypothesis.
Recommended video:
Critical Values: t-Distribution
 Verified step by step guidance
Verified step by step guidance Verified video answer for a similar problem:
Verified video answer for a similar problem: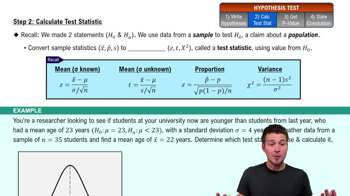

 6:21m
6:21m