Randomization vs t Test Two samples of commute times from Boston and New York are randomly selected and it is found that the samples sizes are n1 = 18 and n2 = 12 and each of the two samples appears to be from a population with a distribution that is dramatically far from normal. Which method is more likely to yield better results for testing Mu1 is not equals to Mu2. Hypothesis test using the t distribution (as in Section 9-2) or the resampling method?
Table of contents
- 1. Intro to Stats and Collecting Data1h 14m
- 2. Describing Data with Tables and Graphs1h 55m
- 3. Describing Data Numerically2h 5m
- 4. Probability2h 16m
- 5. Binomial Distribution & Discrete Random Variables3h 6m
- 6. Normal Distribution and Continuous Random Variables2h 11m
- 7. Sampling Distributions & Confidence Intervals: Mean3h 23m
- Sampling Distribution of the Sample Mean and Central Limit Theorem19m
- Distribution of Sample Mean - Excel23m
- Introduction to Confidence Intervals15m
- Confidence Intervals for Population Mean1h 18m
- Determining the Minimum Sample Size Required12m
- Finding Probabilities and T Critical Values - Excel28m
- Confidence Intervals for Population Means - Excel25m
- 8. Sampling Distributions & Confidence Intervals: Proportion1h 12m
- 9. Hypothesis Testing for One Sample3h 29m
- 10. Hypothesis Testing for Two Samples4h 50m
- Two Proportions1h 13m
- Two Proportions Hypothesis Test - Excel28m
- Two Means - Unknown, Unequal Variance1h 3m
- Two Means - Unknown Variances Hypothesis Test - Excel12m
- Two Means - Unknown, Equal Variance15m
- Two Means - Unknown, Equal Variances Hypothesis Test - Excel9m
- Two Means - Known Variance12m
- Two Means - Sigma Known Hypothesis Test - Excel21m
- Two Means - Matched Pairs (Dependent Samples)42m
- Matched Pairs Hypothesis Test - Excel12m
- 11. Correlation1h 6m
- 12. Regression1h 50m
- 13. Chi-Square Tests & Goodness of Fit1h 57m
- 14. ANOVA1h 57m
9. Hypothesis Testing for One Sample
Steps in Hypothesis Testing
Problem 9.CR.2
Textbook Question
In Exercises 1–10, based on the nature of the given data, do the following:
a. Pose a key question that is relevant to the given data.
b. Identify a procedure or tool from this chapter or the preceding chapters to address the key question from part (a).
c. Analyze the data and state a conclusion.
Video Games In a survey of subjects aged 18–29, subjects were asked if they play video games often or sometimes. Among 984 females, 49% answered “yes” (based on data from a Pew Research Center survey).
 Verified step by step guidance
Verified step by step guidance1
Step 1: Pose a key question relevant to the given data. For example, 'Is there evidence to suggest that the proportion of females aged 18–29 who play video games often or sometimes is significantly different from 50%?' This question focuses on testing whether the observed proportion (49%) differs from a hypothesized proportion (50%).
Step 2: Identify the appropriate statistical procedure or tool to address the key question. Since the problem involves proportions, a hypothesis test for a population proportion (such as a one-sample z-test for proportions) is suitable. This test will help determine if the observed proportion is significantly different from the hypothesized proportion.
Step 3: Set up the null and alternative hypotheses. The null hypothesis (H₀) is that the population proportion of females aged 18–29 who play video games often or sometimes is equal to 50% (p = 0.50). The alternative hypothesis (H₁) is that the population proportion is not equal to 50% (p ≠ 0.50).
Step 4: Calculate the test statistic using the formula for a z-test for proportions: , where p is the sample proportion (0.49), p₀ is the hypothesized proportion (0.50), and n is the sample size (984).
Step 5: Compare the calculated z-value to the critical z-value for the chosen significance level (e.g., α = 0.05). If the absolute value of the calculated z-value exceeds the critical z-value, reject the null hypothesis. Otherwise, fail to reject the null hypothesis. Based on this comparison, state a conclusion about whether the proportion of females aged 18–29 who play video games often or sometimes is significantly different from 50%.
 Verified video answer for a similar problem:
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
4mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Survey Methodology
Survey methodology involves the techniques and processes used to collect data from respondents. In this context, understanding how the survey was conducted, including sample size and demographic targeting, is crucial for interpreting the results accurately. It helps in assessing the reliability and validity of the findings, such as the percentage of females who play video games.
Recommended video:
Guided course

Intro to Random Variables & Probability Distributions Example 1
Statistical Analysis
Statistical analysis refers to the methods used to summarize, interpret, and draw conclusions from data. In this case, analyzing the 49% of females who play video games involves calculating proportions and possibly comparing them to other demographics. This analysis can reveal trends and inform decisions based on the data collected.
Recommended video:
Guided course

Parameters vs. Statistics
Conclusion Drawing
Conclusion drawing is the process of interpreting the results of data analysis to make informed statements or decisions. After analyzing the survey data, one must synthesize the findings to answer the key question posed. This step is essential for translating statistical results into actionable insights, such as understanding gaming habits among young females.
Recommended video:
Guided course
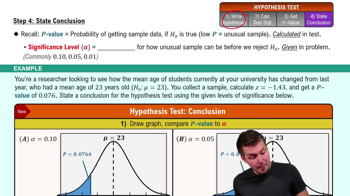
Step 4: State Conclusion

 6:21m
6:21mWatch next
Master Step 1: Write Hypotheses with a bite sized video explanation from Patrick
Start learningRelated Videos
Related Practice
Textbook Question
