Table of contents

1. Intro to Stats and Collecting Data1h 14m
2. Describing Data with Tables and Graphs1h 55m
3. Describing Data Numerically2h 5m
4. Probability2h 16m
5. Binomial Distribution & Discrete Random Variables3h 6m
6. Normal Distribution and Continuous Random Variables2h 11m
7. Sampling Distributions & Confidence Intervals: Mean3h 23m
8. Sampling Distributions & Confidence Intervals: Proportion1h 25m
9. Hypothesis Testing for One Sample3h 29m
10. Hypothesis Testing for Two Samples4h 50m
11. Correlation1h 6m
12. Regression1h 50m
13. Chi-Square Tests & Goodness of Fit1h 57m
14. ANOVA1h 57m

1. Intro to Stats and Collecting Data

Intro to Stats

Statistics

1. Intro to Stats and Collecting Data

Intro to Stats

Previous problemNext problem

1:55 minutes

Problem 2.CRE.4b

Textbook Question

In Exercises 1–5, use the data listed in the margin, which are magnitudes (Richter scale) and depths (km) of earthquakes from Data Set 24 “Earthquakes” in Appendix B
[Image]
Data Type

b. For the listed earthquake depths, are the data categorical or quantitative?

Verified step by step guidance

Understand the difference between categorical and quantitative data: Categorical data represent characteristics or qualities that can be divided into groups, while quantitative data represent numerical values that can be measured and ordered.

Identify the nature of the data in question: The problem refers to earthquake depths, which are measured in kilometers.

Determine if the data are numerical: Since depths are given in kilometers, they are numerical values that can be measured and ordered.

Classify the data type: Since the earthquake depths are numerical and can be measured, they are considered quantitative data.

Conclude that the earthquake depths are quantitative data because they represent measurable numerical values.

Verified video answer for a similar problem:

This video solution was recommended by our tutors as helpful for the problem above

Video duration:

Play a video:

Was this helpful?

Key Concepts

Here are the essential concepts you must grasp in order to answer the question correctly.

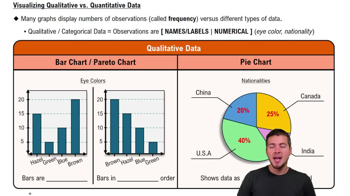
Categorical Data

Categorical data refers to variables that can be divided into distinct categories or groups. These data types are qualitative and describe characteristics or attributes, such as colors, names, or labels. They do not have a numerical value or order, making them unsuitable for arithmetic operations. Examples include gender, type of car, or earthquake classification by region.

Quantitative Data

Quantitative data consists of numerical values that represent quantities or amounts. These data types can be measured and ordered, allowing for arithmetic operations. Quantitative data can be further divided into discrete data, which are countable, and continuous data, which can take any value within a range. Examples include height, weight, and earthquake depths measured in kilometers.

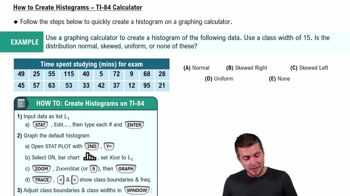
Richter Scale

The Richter scale is a logarithmic scale used to measure the magnitude of earthquakes. It quantifies the energy released by an earthquake, with each whole number increase representing a tenfold increase in measured amplitude and roughly 31.6 times more energy release. Understanding the Richter scale is crucial for interpreting earthquake data, as it provides a standardized method to compare the size of different seismic events.

Watch next

Master Introduction to Statistics Channel with a bite sized video explanation from Patrick

Start learning

Related Videos

Related Practice

Textbook Question

Standard Deviation One way to get a very rough approximation of the value of a standard deviation of sample data is to find the range, then divide it by 4. The range is the difference between the highest sample value and the lowest sample value. In using this approach, what value is obtained from the sample data listed in Exercise 1 “IQ Scores”?

Textbook Question

In Exercises 9–12, the given expressions are designed to yield results expressed in a form of scientific notation. For example, the calculator-displayed result of 1.23E5 can be expressed as 123,000, and the result of 1.23E-4 can be expressed as 0.000123. Perform the indicated operation and express the result as an ordinary number that is not in scientific notation.

(8)^12

Textbook Question

(0.2)^12

Textbook Question

In Exercises 1–5, use the data listed in the margin, which are magnitudes (Richter scale) and depths (km) of earthquakes from Data Set 24 “Earthquakes” in Appendix B

[Image]

Data Type

a. The listed earthquake depths (km) are all rounded to one decimal place. Before rounding, are the exact depths discrete data or continuous data?

Textbook Question

In Exercises 1–5, use the data listed in the margin, which are magnitudes (Richter scale) and depths (km) of earthquakes from Data Set 24 “Earthquakes” in Appendix B

[Image]

Data Type

c. Identify the level of measurement of the listed earthquake depths: nominal, ordinal, interval, or ratio.

Textbook Question

In Exercises 1–5, use the data listed in the margin, which are magnitudes (Richter scale) and depths (km) of earthquakes from Data Set 24 “Earthquakes” in Appendix B

[Image]

Data Type

d. Given that the listed earthquake depths are part of a larger collection of depths, do the data constitute a sample or a population?

Textbook Question

Sugar Listed below are measured weights (mg) of sugar in Domino packets labelled as containing 3500 mg (or 3.5 g).

[IMAGE]

d. Given that the weights are from Domino sugar packets selected from a much larger population, are the weights a sample or a population?

Textbook Question

Sampling Eye Color Based on a study by Dr. P. Sorita Soni at Indiana University, assume that eye colors in the United States are distributed as follows: 40% brown, 35% blue, 12% green, 7% gray, 6% hazel.

a. A statistics instructor collects eye color data from her students. What is the name for this type of sample?

Show more practices