Distributions Identify the distribution (normal, Student t, chi-square) that should be used in each of the following situations. If none of the three distributions can be used, what other method could be used?

a. In constructing a confidence interval of , you have 75 sample values and they appear to be from a population with a skewed distribution. The population standard deviation is not known.

Verified step by step guidance

Step 1: Recognize that the problem involves constructing a confidence interval, which typically requires knowledge of the sample size, population distribution, and whether the population standard deviation is known.

Step 2: Note that the sample size is 75, which is relatively large. According to the Central Limit Theorem, for large sample sizes (usually n > 30), the sampling distribution of the sample mean tends to be approximately normal, even if the population distribution is skewed.

Step 3: Observe that the population standard deviation is not known. When the population standard deviation is unknown, the Student's t-distribution is generally used instead of the normal distribution for constructing confidence intervals.

Step 4: Confirm that the Student's t-distribution is appropriate here because it accounts for the additional uncertainty introduced by estimating the population standard deviation using the sample standard deviation.

Step 5: Conclude that the Student's t-distribution should be used in this situation to construct the confidence interval, as it is suitable for large sample sizes and unknown population standard deviation.

Verified video answer for a similar problem:

This video solution was recommended by our tutors as helpful for the problem above

Video duration:

Was this helpful?

Key Concepts

Here are the essential concepts you must grasp in order to answer the question correctly.

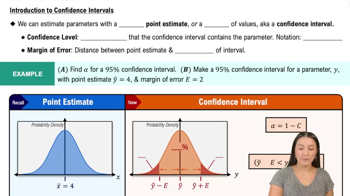
Confidence Interval

A confidence interval is a range of values, derived from sample statistics, that is likely to contain the true population parameter. It provides an estimate of uncertainty around a sample mean or proportion. The width of the interval depends on the sample size and variability, and it is typically expressed at a certain confidence level, such as 95%.

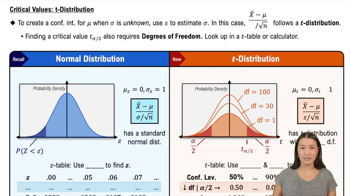
Student's t-distribution

The Student's t-distribution is a probability distribution used when estimating population parameters when the sample size is small and the population standard deviation is unknown. It is similar to the normal distribution but has heavier tails, which accounts for the increased variability expected in smaller samples. This makes it particularly useful for constructing confidence intervals and hypothesis testing in such scenarios.

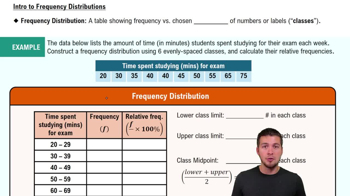
Skewed Distribution

A skewed distribution is one where the data points are not symmetrically distributed around the mean, leading to a longer tail on one side. In a right-skewed distribution, for example, the majority of values cluster on the left, with a few larger values stretching the tail to the right. Understanding the skewness of data is crucial for selecting appropriate statistical methods, as it can affect the validity of assumptions underlying certain tests.

Watch next

Master Introduction to Confidence Intervals with a bite sized video explanation from Patrick

Start learning