Boxplot Using the same differences from Exercise 1, construct a boxplot and include the values of the 5-number summary.
Table of contents
- 1. Intro to Stats and Collecting Data1h 14m
- 2. Describing Data with Tables and Graphs1h 55m
- 3. Describing Data Numerically2h 5m
- 4. Probability2h 16m
- 5. Binomial Distribution & Discrete Random Variables3h 6m
- 6. Normal Distribution and Continuous Random Variables2h 11m
- 7. Sampling Distributions & Confidence Intervals: Mean3h 23m
- Sampling Distribution of the Sample Mean and Central Limit Theorem19m
- Distribution of Sample Mean - Excel23m
- Introduction to Confidence Intervals15m
- Confidence Intervals for Population Mean1h 18m
- Determining the Minimum Sample Size Required12m
- Finding Probabilities and T Critical Values - Excel28m
- Confidence Intervals for Population Means - Excel25m
- 8. Sampling Distributions & Confidence Intervals: Proportion1h 25m
- 9. Hypothesis Testing for One Sample3h 29m
- 10. Hypothesis Testing for Two Samples4h 50m
- Two Proportions1h 13m
- Two Proportions Hypothesis Test - Excel28m
- Two Means - Unknown, Unequal Variance1h 3m
- Two Means - Unknown Variances Hypothesis Test - Excel12m
- Two Means - Unknown, Equal Variance15m
- Two Means - Unknown, Equal Variances Hypothesis Test - Excel9m
- Two Means - Known Variance12m
- Two Means - Sigma Known Hypothesis Test - Excel21m
- Two Means - Matched Pairs (Dependent Samples)42m
- Matched Pairs Hypothesis Test - Excel12m
- 11. Correlation1h 6m
- 12. Regression1h 50m
- 13. Chi-Square Tests & Goodness of Fit1h 57m
- 14. ANOVA1h 57m
3. Describing Data Numerically
Describing Data Numerically Using a Graphing Calculator
Problem 10.1.10a
Textbook Question
Clusters Refer to the Minitab-generated scatterplot. The four points in the lower left corner are measurements from women, and the four points in the upper right corner are from men.
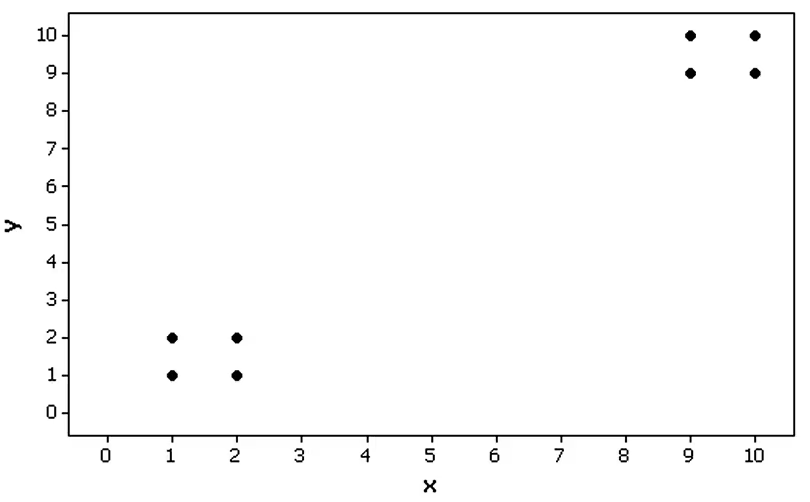
a. Examine the pattern of the four points in the lower left corner (from women) only, and subjectively determine whether there appears to be a correlation between x and y for women.
 Verified step by step guidance
Verified step by step guidance1
Step 1: Observe the scatterplot and focus on the four points in the lower left corner, which represent measurements from women. These points are located in the region where both x and y values are relatively small.
Step 2: Analyze the pattern of these four points. Check if there is a visible trend or relationship between the x-values (horizontal axis) and y-values (vertical axis). For example, determine if the points seem to increase or decrease together, or if they appear randomly scattered.
Step 3: Consider the concept of correlation. Correlation measures the strength and direction of a linear relationship between two variables. If the points form a clear upward or downward trend, there may be a positive or negative correlation, respectively. If the points are scattered without any discernible pattern, the correlation may be weak or nonexistent.
Step 4: Subjectively assess the alignment of the points. For example, if the x-values increase while the y-values remain relatively constant, this suggests no correlation. If both x and y values increase or decrease together, this suggests a positive or negative correlation.
Step 5: Conclude your subjective determination based on the visual inspection of the scatterplot. Note that this is a qualitative assessment and does not involve calculating the correlation coefficient, which would require numerical data.
 Verified video answer for a similar problem:
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
4mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Scatterplot
A scatterplot is a graphical representation of two variables, where each point represents an observation in the dataset. The x-axis typically represents one variable, while the y-axis represents another. By plotting the data points, one can visually assess the relationship between the two variables, such as correlation, trends, or clusters.
Recommended video:
Guided course
Scatterplots & Intro to Correlation
Correlation
Correlation refers to the statistical relationship between two variables, indicating how one variable may change in relation to another. It can be positive, negative, or zero, with positive correlation meaning that as one variable increases, the other does as well, and negative correlation indicating that as one increases, the other decreases. Correlation is often quantified using the correlation coefficient, which ranges from -1 to 1.
Recommended video:
Guided course
Correlation Coefficient
Subjective Analysis
Subjective analysis involves interpreting data based on personal judgment rather than strict statistical methods. In the context of examining a scatterplot, it means assessing the visual patterns and relationships between points without relying solely on numerical measures. This approach can provide insights into trends or anomalies that may not be immediately evident through quantitative analysis.
Recommended video:
Guided course

Difference in Proportions: Hypothesis Tests

 4:51m
4:51mWatch next
Master Find 5-Number Summary - TI-84 Calculator with a bite sized video explanation from Patrick
Start learningRelated Videos
Related Practice
Textbook Question
