You take a 6-question quiz with True/False questions. What is the probability of getting all 6 questions correct by simply guessing?
Table of contents
- 1. Intro to Stats and Collecting Data1h 14m
- 2. Describing Data with Tables and Graphs1h 55m
- 3. Describing Data Numerically2h 5m
- 4. Probability2h 16m
- 5. Binomial Distribution & Discrete Random Variables3h 6m
- 6. Normal Distribution and Continuous Random Variables2h 11m
- 7. Sampling Distributions & Confidence Intervals: Mean3h 23m
- Sampling Distribution of the Sample Mean and Central Limit Theorem19m
- Distribution of Sample Mean - Excel23m
- Introduction to Confidence Intervals15m
- Confidence Intervals for Population Mean1h 18m
- Determining the Minimum Sample Size Required12m
- Finding Probabilities and T Critical Values - Excel28m
- Confidence Intervals for Population Means - Excel25m
- 8. Sampling Distributions & Confidence Intervals: Proportion1h 12m
- 9. Hypothesis Testing for One Sample3h 29m
- 10. Hypothesis Testing for Two Samples4h 50m
- Two Proportions1h 13m
- Two Proportions Hypothesis Test - Excel28m
- Two Means - Unknown, Unequal Variance1h 3m
- Two Means - Unknown Variances Hypothesis Test - Excel12m
- Two Means - Unknown, Equal Variance15m
- Two Means - Unknown, Equal Variances Hypothesis Test - Excel9m
- Two Means - Known Variance12m
- Two Means - Sigma Known Hypothesis Test - Excel21m
- Two Means - Matched Pairs (Dependent Samples)42m
- Matched Pairs Hypothesis Test - Excel12m
- 11. Correlation1h 6m
- 12. Regression1h 50m
- 13. Chi-Square Tests & Goodness of Fit1h 57m
- 14. ANOVA1h 57m
5. Binomial Distribution & Discrete Random Variables
Binomial Distribution
Problem 5.1.22
Textbook Question
Texting and Driving. In Exercises 21–26, refer to the accompanying table, which describes probabilities for groups of five drivers. The random variable x is the number of drivers in a group who say that they text while driving (based on data from an Arity survey of drivers).
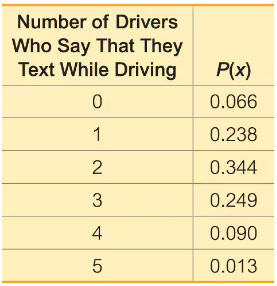
Range Rule of Thumb for Significant Events Use the range rule of thumb to determine whether 4 is a significantly high number of drivers who say that they text while driving.
 Verified step by step guidance
Verified step by step guidance1
Step 1: Understand the Range Rule of Thumb. This rule states that values are considered significantly high if they are greater than or equal to the mean plus two standard deviations, and significantly low if they are less than or equal to the mean minus two standard deviations.
Step 2: Calculate the mean (μ) of the random variable x. Use the formula μ = Σ[x * P(x)], where x represents the number of drivers and P(x) represents the probability associated with each x value.
Step 3: Calculate the standard deviation (σ) using the formula σ = √Σ[(x - μ)^2 * P(x)]. This measures the spread of the data around the mean.
Step 4: Determine the threshold for significantly high values using the formula μ + 2σ. Compare the value of 4 (the number of drivers who say they text while driving) to this threshold.
Step 5: Interpret the result. If 4 is greater than or equal to μ + 2σ, it is considered significantly high. Otherwise, it is not considered significantly high.
 Verified video answer for a similar problem:
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
3mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Random Variable
A random variable is a numerical outcome of a random phenomenon. In this context, the random variable x represents the number of drivers in a group of five who report texting while driving. Understanding random variables is crucial for analyzing probabilities and making inferences about populations based on sample data.
Recommended video:
Guided course
Intro to Random Variables & Probability Distributions
Probability Distribution
A probability distribution describes how probabilities are assigned to each possible value of a random variable. The table provided shows the probability distribution for the random variable x, indicating the likelihood of 0 to 5 drivers texting while driving. This distribution is essential for calculating expected values and assessing the significance of observed outcomes.
Recommended video:
Guided course

Calculating Probabilities in a Binomial Distribution
Range Rule of Thumb
The range rule of thumb is a guideline used to determine whether a value is significantly high or low in a given context. It suggests that values beyond two standard deviations from the mean can be considered significant. In this case, applying the range rule helps assess whether having 4 drivers texting while driving is an unusual occurrence based on the provided probabilities.
Recommended video:
Probability of Mutually Exclusive Events

 6:00m
6:00mWatch next
Master The Binomial Experiment with a bite sized video explanation from Patrick
Start learningRelated Videos
Related Practice
Multiple Choice
