Here are the essential concepts you must grasp in order to answer the question correctly.
Poisson Distribution
The Poisson distribution is a probability distribution that expresses the probability of a given number of events occurring in a fixed interval of time or space, given a known average rate of occurrence. It is particularly useful for modeling rare events, such as natural disasters, where the events occur independently. The formula for the Poisson probability mass function is P(X=k) = (λ^k * e^(-λ)) / k!, where λ is the average rate, k is the number of occurrences, and e is Euler's number.
Recommended video:
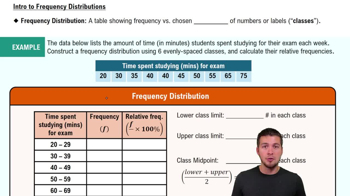
Intro to Frequency Distributions
Mean (λ)
In the context of the Poisson distribution, the mean (denoted as λ) represents the average number of occurrences of the event in a specified interval. For this question, λ is given as 5.5, indicating that, on average, there are 5.5 hurricanes per year in the United States. This parameter is crucial for calculating the probabilities of different outcomes using the Poisson formula.
Recommended video:
Probability Calculation
To find the probability of a specific number of events occurring in a Poisson distribution, one uses the Poisson probability mass function. For this question, to find the probability of exactly 7 hurricanes in a year, you would substitute k=7 and λ=5.5 into the formula. This calculation will yield the likelihood of observing that exact number of hurricanes, which is essential for understanding the variability and risk associated with hurricane occurrences.
Recommended video:
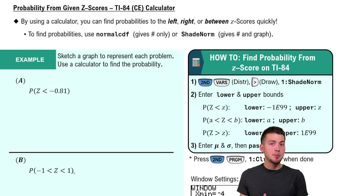
Probability From Given Z-Scores - TI-84 (CE) Calculator