Table of contents

1. Intro to Stats and Collecting Data55m
2. Describing Data with Tables and Graphs1h 55m
3. Describing Data Numerically1h 45m
4. Probability2h 16m
5. Binomial Distribution & Discrete Random Variables2h 33m
6. Normal Distribution and Continuous Random Variables1h 38m
7. Sampling Distributions & Confidence Intervals: Mean1h 53m
8. Sampling Distributions & Confidence Intervals: Proportion1h 12m
- Sampling Distribution of Sample Proportion
  29m
- Confidence Intervals for Population Proportion
  42m
9. Hypothesis Testing for One Sample2h 19m
10. Hypothesis Testing for Two Samples3h 22m
11. Correlation1h 6m
12. Regression1h 4m
13. Chi-Square Tests & Goodness of Fit1h 20m
14. ANOVA1h 0m

5. Binomial Distribution & Discrete Random Variables

Discrete Random Variables

Statistics

5. Binomial Distribution & Discrete Random Variables

Discrete Random Variables

Previous problemNext problem

2:54 minutes

Problem 5.Q.4

Textbook Question

Find the mean of the random variable x described in the preceding exercise.

Verified step by step guidance

Step 1: Recall the formula for the mean (expected value) of a random variable x. The mean is calculated as \( \mu = \sum_{i} x_i P(x_i) \), where \( x_i \) represents the values of the random variable and \( P(x_i) \) represents their corresponding probabilities.

Step 2: Identify the values of \( x_i \) (the possible outcomes of the random variable) and \( P(x_i) \) (the probabilities associated with each outcome) from the preceding exercise.

Step 3: Multiply each value \( x_i \) by its corresponding probability \( P(x_i) \). This gives the weighted contribution of each outcome to the mean.

Step 4: Sum all the weighted contributions \( \sum_{i} x_i P(x_i) \) to compute the mean of the random variable.

Step 5: Ensure that the probabilities \( P(x_i) \) sum to 1, as this is a requirement for a valid probability distribution. If they do not, revisit the preceding exercise to verify the probabilities.

Verified video answer for a similar problem:

This video solution was recommended by our tutors as helpful for the problem above

Video duration:

Play a video:

Was this helpful?

Key Concepts

Here are the essential concepts you must grasp in order to answer the question correctly.

Mean

The mean, often referred to as the average, is a measure of central tendency that summarizes a set of values by dividing the sum of all values by the number of values. In the context of a random variable, the mean represents the expected value, indicating where the center of the distribution lies. It is a crucial concept in statistics as it provides a single value that represents the entire dataset.

Random Variable

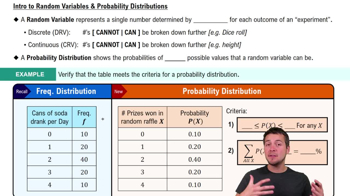
A random variable is a numerical outcome of a random phenomenon, which can take on different values based on the outcome of a random event. Random variables can be discrete, taking on specific values, or continuous, taking on any value within a range. Understanding random variables is essential for calculating probabilities and statistical measures like the mean.

Expected Value

The expected value of a random variable is a fundamental concept in probability and statistics that represents the long-term average of the variable's outcomes. It is calculated by multiplying each possible outcome by its probability and summing these products. The expected value provides insight into the average result one can anticipate from a random variable over numerous trials.

Watch next

Master Intro to Random Variables & Probability Distributions with a bite sized video explanation from Patrick

Start learning

Related Videos

Related Practice

Textbook Question

In Exercises 5–8, assume that the Poisson distribution applies; assume that the mean number of Atlantic hurricanes in the United States is 5.5 per year, as in Example 1; and proceed to find the indicated probability.

a. Find the probability that in a year, there will be no hurricanes.

Textbook Question

b. In a 118-year period, how many years are expected to have no hurricanes?

Textbook Question

a. Find the probability that in a year, there will be 10 hurricanes.

Textbook Question

b. In a 118-year period, how many years are expected to have 10 hurricanes?

Textbook Question

Is the mean found in the preceding exercise a statistic or a parameter?

Textbook Question

Poisson: Deaths Currently, an average of 7 residents of the village of Westport (population 760) die each year (based on data from the U.S. National Center for Health Statistics).

a. Find the mean number of deaths per day.

Textbook Question

Poisson: Deaths Currently, an average of 7 residents of the village of Westport (population 760) die each year (based on data from the U.S. National Center for Health Statistics).

b. Find the probability that on a given day, there are no deaths.

Textbook Question

Poisson: Deaths Currently, an average of 7 residents of the village of Westport (population 760) die each year (based on data from the U.S. National Center for Health Statistics).

c. Find the probability that on a given day, there is more than one death.

Show more practices

Download the Mobile app

Privacy

Do not sell my personal information

Accessibility

Patent notice

Sitemap