Solve each rational inequality. Give the solution set in interval notation. (2x - 3)/(x + 1) > 4

Show that the real zeros of each polynomial function satisfy the given conditions. See Example 6.

$\text{ƒ}\left(x\right)=x^5+2x^3-2x^2+5x+5$; no real zero less than -1

Graph each rational function. ƒ(x)=(x+1)/(x-4)

Solve each rational inequality. Give the solution set in interval notation. $\frac{x^2-3x-4}{x^2+6x+9}\le 0$

Find a polynomial function ƒ(x) of least degree having only real coefficients and zeros as given. Assume multiplicity 1 unless otherwise stated. 5+i and 5-i

Use synthetic division to determine whether the given number k is a zero of the polynomial function. If it is not, give the value of ƒ(k). ƒ(x) = 4x⁴ + x² + 17x + 3; k= -3/2

Show that the real zeros of each polynomial function satisfy the given conditions. ƒ(x)=3x⁴+2x³-4x²+x-1; no real zero greater than 1

Show that the real zeros of each polynomial function satisfy the given conditions. See Example 6.

$\text{ƒ}\left(x\right)=3x^4+2x^3-4x^2+x-1$; no real zero less than -2

Use synthetic division to determine whether the given number k is a zero of the polynomial function. If it is not, give the value of ƒ(k). ƒ(x) = x³ + 3x² -x + 1; k = 1+i

Show that the real zeros of each polynomial function satisfy the given conditions. ƒ(x)=x⁵-3x³+x+2; no real zero greater than 2

Graph each rational function. ƒ(x)=(x+2)/(x-3)

Solve each rational inequality. Give the solution set in interval notation. 1 /(x+ 2) > 1 /(x -3)

Show that the real zeros of each polynomial function satisfy the given conditions. See Example 6.

$\text{ƒ}\left(x\right)=x^5-3x^3+x+2$; no real zero less than -3

Solve each rational inequality. Give the solution set in interval notation. 1 /(x - 1) < 1 /(x + 1)

Solve each rational inequality. Give the solution set in interval notation. 2 /(x - 2) ≥ 1 / x

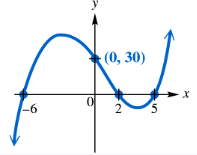
Find a polynomial function f of least degree having the graph shown. (Hint: See the NOTE following Example 4.)



The remainder theorem indicates that when a polynomial ƒ(x) is divided by x-k, the remainder is equal to ƒ(k). Consider the polynomial function ƒ(x) = x³ - 2x² - x+2. Use the remainder theorem to find each of the following. Then determine the coordinates of the corresponding point on the graph of ƒ(x). ƒ (-2)

Graph each rational function. ƒ(x)=4/(x-1)

Solve each rational inequality. Give the solution set in interval notation. See Examples 4 and 5.

$\frac{5}{x+3}\ge \frac{3}{x}$

Graph each rational function. ƒ(x)=(6-3x)/(4-x)

Graph each rational function. ƒ(x)=3x/(x²-x-2)

Solve each rational inequality. Give the solution set in interval notation. 3 /{4 - x} > 6 /{ 1 - x}

Find a polynomial function ƒ(x) of least degree having only real coefficients and zeros as given. Assume multiplicity 1 unless otherwise stated. 2-i, 3, and -1

Solve each rational inequality. Give the solution set in interval notation.

$\frac{5}{2-x}>\frac{3}{3-x}$

Graph each rational function. ƒ(x)=(2x+1)/(x²+6x+8)

Graph each rational function. ƒ(x)=5x/(x²-1)

The remainder theorem indicates that when a polynomial ƒ(x) is divided by x-k, the remainder is equal to ƒ(k). Consider the polynomial function ƒ(x) = x³ - 2x² - x+2. Use the remainder theorem to find each of the following. Then determine the coordinates of the corresponding point on the graph of ƒ(x). ƒ (1)

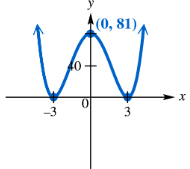
Find a polynomial function f of least degree having the graph shown. (Hint: See the NOTE following Example 4.)

Solve each rational inequality. Give the solution set in interval notation. 1 /{x² - 4x + 3} ≤ 1 /{ 3 - x}

Graph each rational function. See Examples 5–9.

$\text{ƒ}\left(x\right)=x/(4-x^2)$