Back
BackProblem 53
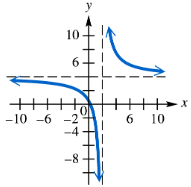
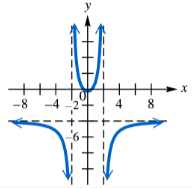
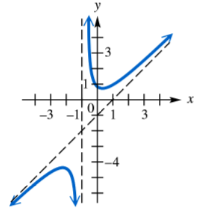
Identify any vertical, horizontal, or oblique asymptotes in the graph of y=ƒ(x). State the domain of ƒ.
Problem 53
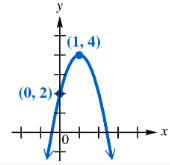
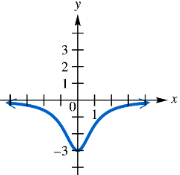
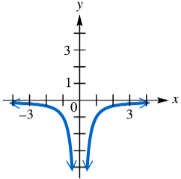
Connecting Graphs with Equations Find a quadratic function f having the graph shown. (Hint: See the Note following Example 3.)
Problem 53
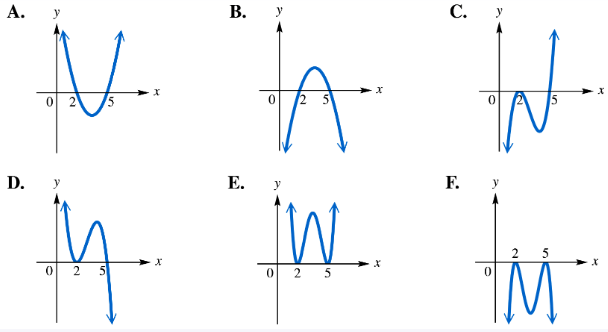
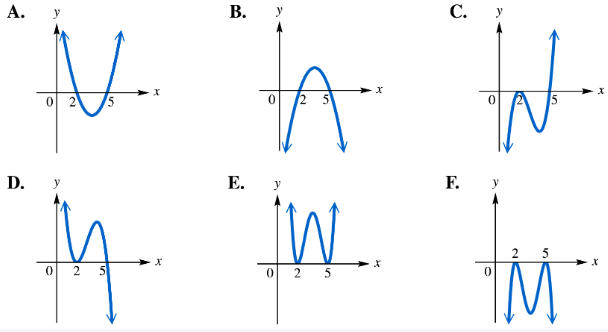
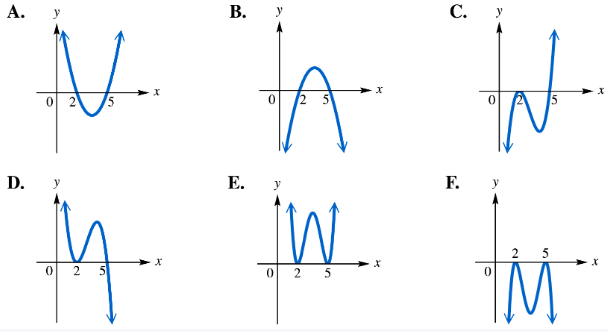
For each polynomial function, identify its graph from choices A–F. ƒ(x)=(x-2)2(x-5)
Problem 53
Solve each rational inequality. Give the solution set in interval notation. (x - 1)/(x - 4) > 0
Problem 53
Find a polynomial function ƒ(x) of degree 3 with real coefficients that satisfies the given conditions. Zeros of -3, 1, and 4; ƒ(2)=30
Problem 53
Use synthetic division to determine whether the given number k is a zero of the polynomial function. If it is not, give the value of ƒ(k). ƒ(x) = x3 +7x2 + 10x; k=0
Problem 54
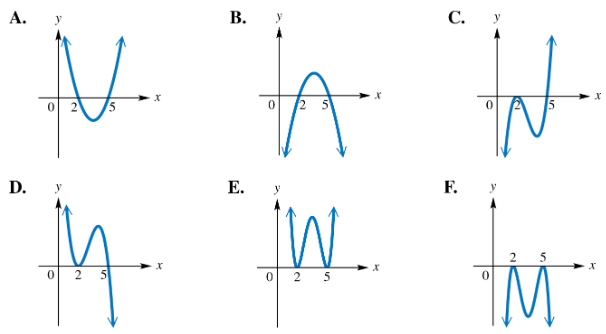
For each polynomial function, identify its graph from choices A–F.
Problem 54
What happens to y if y varies directly as x, and x is halved?
Problem 54
Solve each rational inequality. Give the solution set in interval notation. (x + 1)/(x - 5) > 0
Problem 55
Solve each rational inequality. Give the solution set in interval notation. (2x + 3)/(x - 5) ≤ 0
Problem 55
Find a polynomial function ƒ(x) of degree 3 with real coefficients that satisfies the given conditions. Zeros of -2, 1, and 0; ƒ(-1)=-1
Problem 55
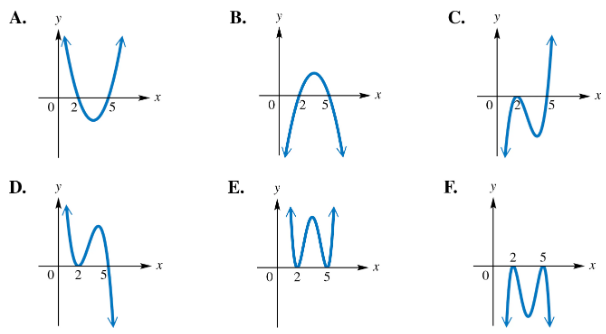
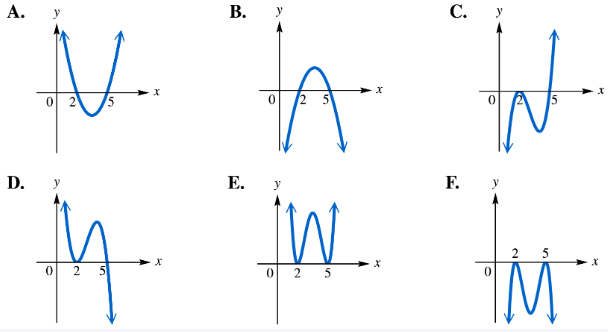
For each polynomial function, identify its graph from choices A–F. ƒ(x)=(x-2)2(x-5)2
Problem 55
Use synthetic division to determine whether the given number k is a zero of the polynomial function. If it is not, give the value of ƒ(k). ƒ(x) = 5x4 + 2x3 -x+3; k=2/5
Problem 55
Identify any vertical, horizontal, or oblique asymptotes in the graph of y=ƒ(x). State the domain of ƒ.
Problem 56
For each polynomial function, identify its graph from choices A–F.
Problem 56
Solve each rational inequality. Give the solution set in interval notation. (3x + 7)/(x - 3) ≤ 0
Problem 57
Show that the real zeros of each polynomial function satisfy the given conditions. ƒ(x)=x4-x3+3x2-8x+8; no real zero greater than 2
Problem 57
For each polynomial function, identify its graph from choices A–F. ƒ(x)=-(x-2)(x-5)
Problem 57
Find a polynomial function ƒ(x) of degree 3 with real coefficients that satisfies the given conditions. Zero of -3 having multiplicity 3; ƒ(3)=36
Problem 57
Identify any vertical, horizontal, or oblique asymptotes in the graph of y=ƒ(x). State the domain of ƒ.
Problem 57
Use synthetic division to determine whether the given number k is a zero of the polynomial function. If it is not, give the value of ƒ(k). ƒ(x) = x2 - 2x + 2; k = 1-i
Problem 57
Solve each rational inequality. Give the solution set in interval notation. 8 /(x - 2) ≥ 2
Problem 58
Show that the real zeros of each polynomial function satisfy the given conditions. ƒ(x)=2x5-x4+2x3-2x2+4x-4; no real zero greater than 1
Problem 58
For each polynomial function, identify its graph from choices A–F. ƒ(x)=-(x-2)2(x-5)2
Problem 58
Identify any vertical, horizontal, or oblique asymptotes in the graph of . State the domain of .
Problem 58
Solve each rational inequality. Give the solution set in interval notation. 20/(x - 1) ≥ 1
Problem 59
Show that the real zeros of each polynomial function satisfy the given conditions. ƒ(x)=x4+x3-x2+3; no real zero less than -2
Problem 59
Solve each rational inequality. Give the solution set in interval notation. (x - 8)/(x - 4) < 3
Problem 59
Use synthetic division to determine whether the given number k is a zero of the polynomial function. If it is not, give the value of ƒ(k). ƒ(x) = x2 + 3x + 4; k = 2+i
Problem 59
Identify any vertical, horizontal, or oblique asymptotes in the graph of y=ƒ(x). State the domain of ƒ.