Use the Binomial Theorem to expand each expression and write the result in simplified form. (x^1/3 +x^-1/3)³

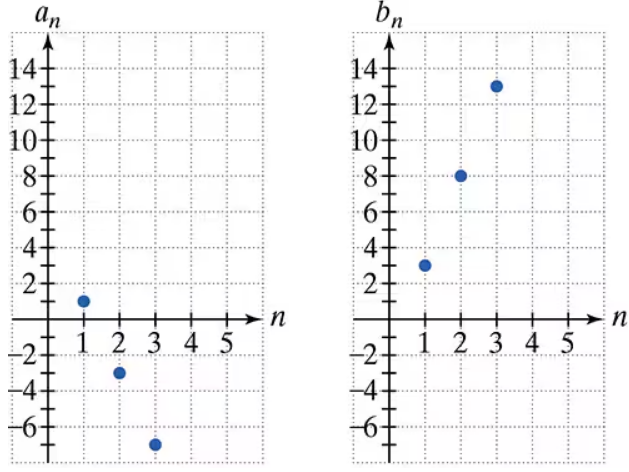
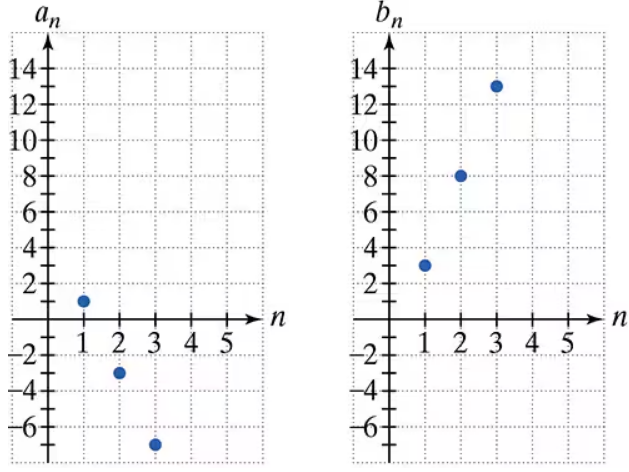
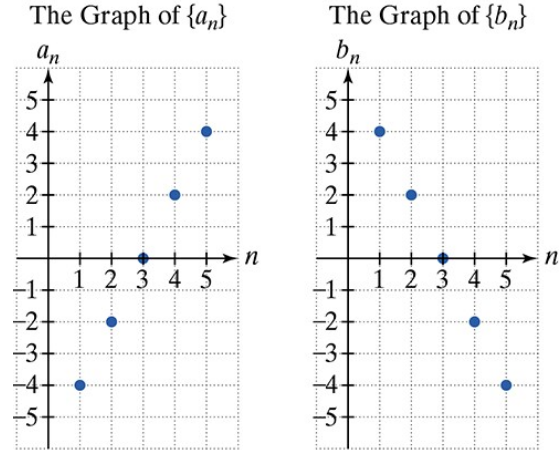
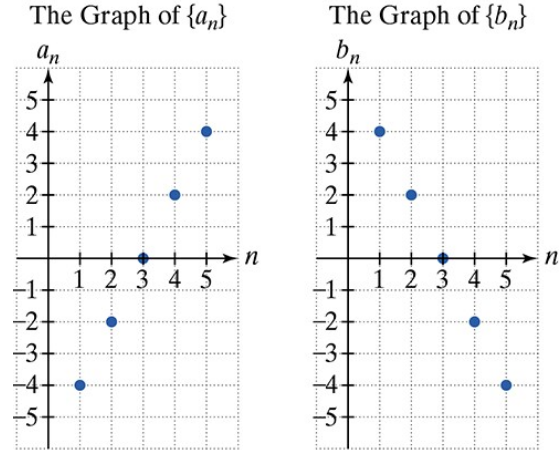
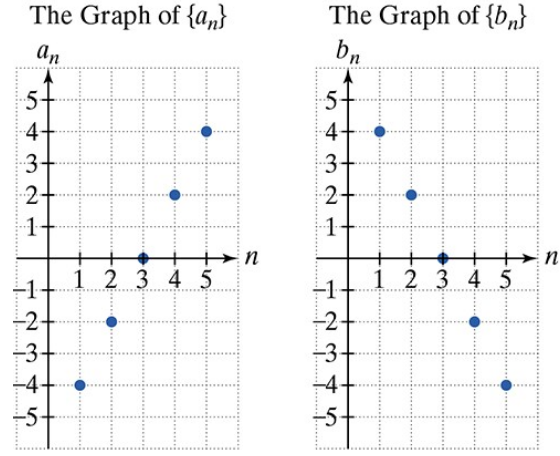
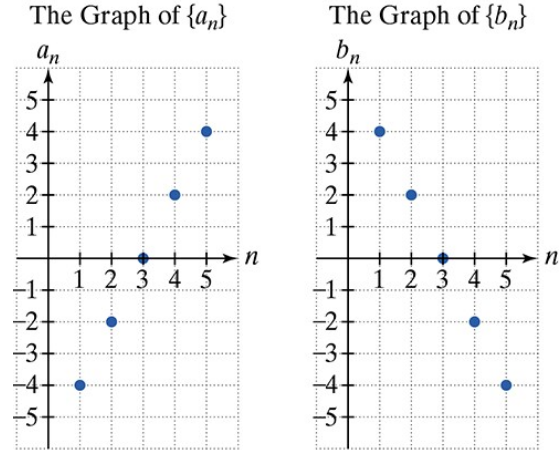
Use the graphs of the arithmetic sequences {a} and {b} to solve Exercises 51-58. If {a_n} is a finite sequence whose last term is -83, how many terms does {a_n} contain?

In Exercises 51–56, the general term of a sequence is given. Determine whether the sequence is arithmetic, geometric, or neither. If the sequence is arithmetic, find the common difference; if it is geometric, find the common ratio. a_n = 2ⁿ

Use the formula for nCr to solve Exercises 49–56. You volunteer to help drive children at a charity event to the zoo, but you can fit only 8 of the 17 children present in your van. How many different groups of 8 children can you drive?

Find f(x + h) − f(x)/h and simplify. f(x) = x⁴+7

In Exercises 43–54, express each sum using summation notation. Use 1 as the lower limit of summation and i for the index of summation. 1+3+5+⋯+ (2n−1)

If you toss a fair coin six times, what is the probability of getting all heads?

Use the formula for nCr to solve Exercises 49–56. To win at LOTTO in the state of Florida, one must correctly select 6 numbers from a collection of 53 numbers (1 through 53). The order in which the selection is made does not matter. How many different selections are possible?

In Exercises 55–60, express each sum using summation notation. Use a lower limit of summation of your choice and k for the index of summation. 5+7+9+11+⋯+ 31

Use the graphs of the arithmetic sequences {a} and {b} to solve Exercises 51-58. Find the difference between the sum of the first 14 terms of {b_n} and the sum of the first 14 terms of {a_n}.

Find the middle term in the expansion of (3/x + x/3)¹⁰

The general term of a sequence is given. Determine whether the sequence is arithmetic, geometric, or neither. If the sequence is arithmetic, find the common difference; if it is geometric, find the common ratio. a_n = n² + 5

Let {a_n} = - 5, 10, - 20, 40, ..., {b_n} = 10, - 5, - 20, - 35, ..., {c_n} = - 2, 1, - 1/2, 1/4 Find a₁₀ + b₁₀.

Express each sum using summation notation. Use a lower limit of summation of your choice and k for the index of summation. a+ar+ar²+⋯+ ar¹²

Use mathematical induction to prove that the statement is true for every positive integer n. 5 + 10 + 15 + ... + 5n = (5n(n+1))/2

Use mathematical induction to prove that the statement is true for every positive integer n. 1 + 4 + 4^2 + ... + 4^(n-1) = ((4^n)-1)/3

In Exercises 55–60, express each sum using summation notation. Use a lower limit of summation of your choice and k for the index of summation. $a+(a+d)+(a+2d)+\cdots +(a+nd)$

Let {a_n} = - 5, 10, - 20, 40, ..., {b_n} = 10, - 5, - 20, - 35, ..., {c_n} = - 2, 1, - 1/2, 1/4 Find the difference between the sum of the first 10 terms of {a_n} and the sum of the first 10 terms of {b_n}.

Let {a_n} = - 5, 10, - 20, 40, ..., {b_n} = 10, - 5, - 20, - 35, ..., {c_n} = - 2, 1, - 1/2, 1/4 Find the difference between the sum of the first 6 terms of {a_n} and the sum of the infinite seris containing all the terms of {c_n}.

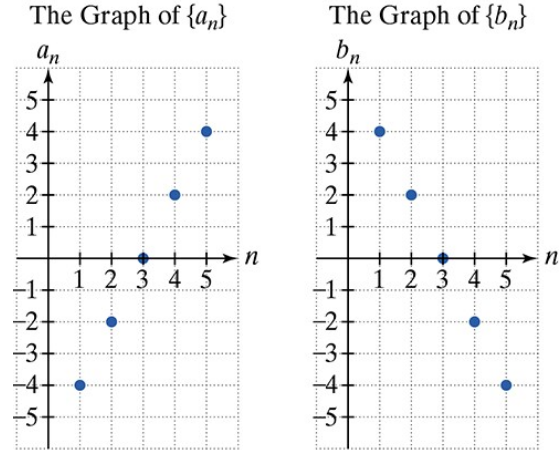
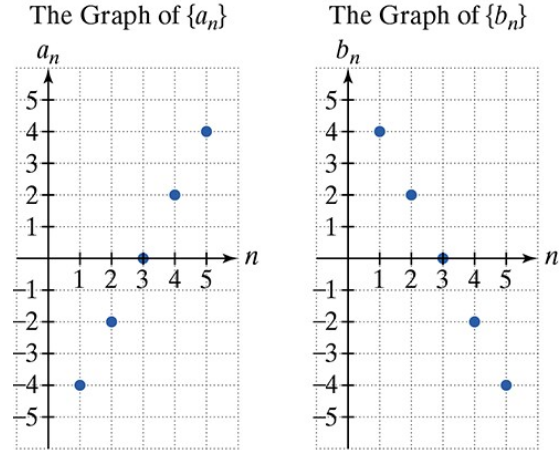
In Exercises 61–68, use the graphs of and to find each indicated sum.

${\sum }_{i=1}^5(a_i^2+1)$

Evaluate the given binomial coefficient 11 8

In Exercises 61–68, use the graphs of and to find each indicated sum.

${\sum }_{i=1}^5(2a_i+b_i)$

Find a₂ and a₃ for each geometric sequence. 8, a₂, a₃, 27

Find a₂ and a₃ for each geometric sequence. 2, a₂, a₃, - 54

Use the Binomial Theorem to expand the binomial and express the result in simplified form. (2x+1)^3

In Exercises 61–68, use the graphs of and to find each indicated sum.

${\sum }_{i=1}^5(a_i+3b_i)$

In Exercises 61–68, use the graphs of and to find each indicated sum.

${\sum }_{i=4}^5(a_i/b_i{)}^2$

Use the Binomial Theorem to expand the binomial and express the result in simplified form. ((x^2)-1)^4

In Exercises 61–68, use the graphs of and to find each indicated sum.

${\sum }_{i=4}^5(a_i/b_i{)}^3$

In Exercises 61–68, use the graphs of and to find each indicated sum.

${\sum }_{i=1}^5{a}_i^2+{\sum }_{i=1}^5{b}_i^2$