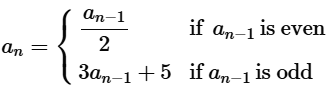How many four-digit odd numbers less than 6000 can be formed using the digits 2, 4, 6, 7, 8, and 9?

Retaining the Concepts. Solve and determine whether 8(x - 3) + 4 = 8x - 21 is an identity, a conditional equation, or an inconsistent equation.

Retaining the Concepts. If f(x) = 4x² - 5x - 2, find [f(x + h) - f(x)]/h, h ≠ 0

What is the probability of a family having five boys born in a row? (Assume the probability of a male birth is 1/2.)

Retaining the Concepts. Expand: ${\log }_7\left(\frac{5\sqrt{x}}{49y^{10}}\right)$

The probability of a flood in any given year in a region prone to floods is 0.2. What is the probability of a flood two years in a row?

The probability of a flood in any given year in a region prone to floods is 0.2. What is the probability of a flood for three consecutive years?

The probability of a flood in any given year in a region prone to floods is 0.2. What is the probability of no flooding for four consecutive years?

Write the first five terms of the sequence whose first term is 9 and whose general term is

for n≥2.

Solve: x/(x−3)=2x/(x−3)−5/3

Use the formula $a_n=4+(n-1)(-7)$ to find the eighth term of the sequence $4,-3,-10,\dots$