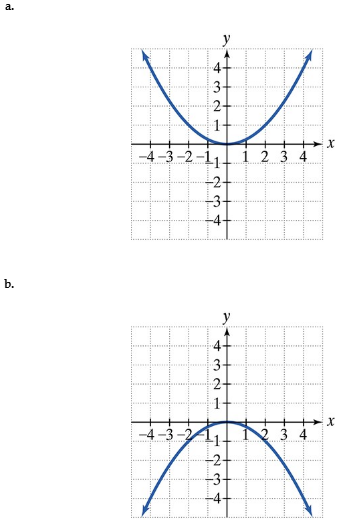
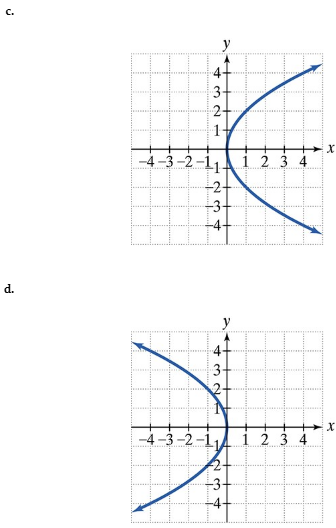
Find the focus and directrix of each parabola with the given equation. Then match each equation to one of the graphs that are shown and labeled (a)–(d).

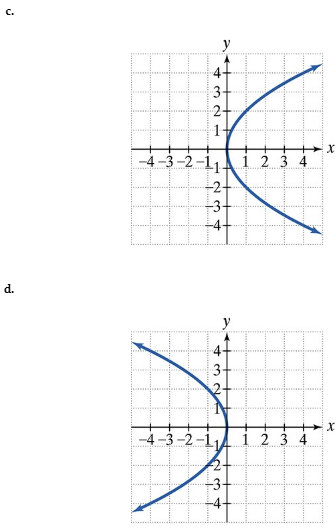
a. b. c. d.

y² = 4x

Graph each ellipse and locate the foci. x²/16+y²/4 = 1

Graph the ellipse and locate the foci. $\frac{x^2}{36}+\frac{y^2}{25}=1$

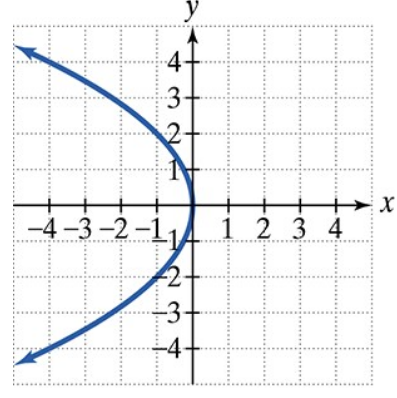
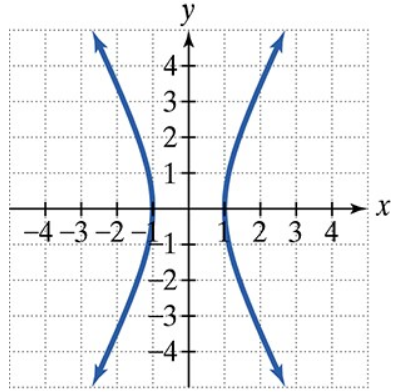
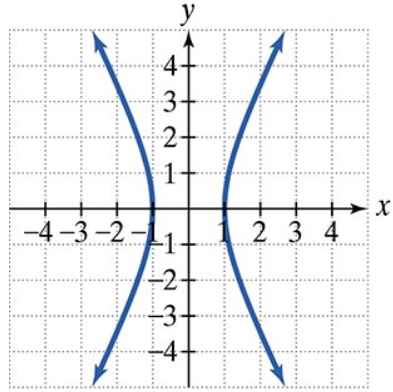
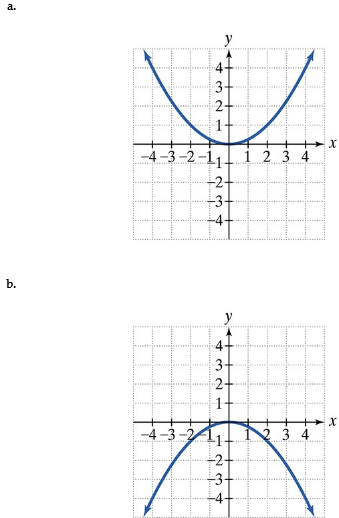
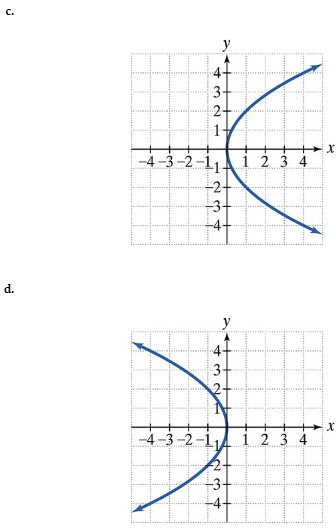
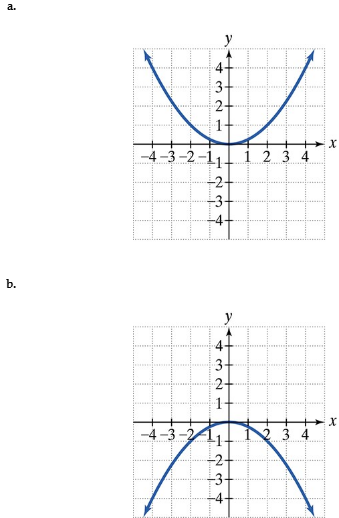
Find the vertices and locate the foci of each hyperbola with the given equation. Then match each equation to one of the graphs that are shown and labeled (a)–(d).

a. b. c. d.

x²/4−y²/1=1

Graph the ellipse and locate the foci. (y^2)/25 + (x^2)/16 = 1

In Exercises 1–4, find the focus and directrix of each parabola with the given equation. Then match each equation to one of the graphs that are shown and labeled (a)–(d). x^2 = 4y

Graph each ellipse and locate the foci. x²/9 +y²/36= 1

Find the vertices and locate the foci of each hyperbola with the given equation. Then match each equation to one of the graphs that are shown and labeled (a)–(d).

a. b. c. d.

y²/4−x²/1=1

Graph the ellipse and locate the foci. 9x^2 + 4y^2 - 18x + 8y -23 = 0

In Exercises 1–4, find the focus and directrix of each parabola with the given equation. Then match each equation to one of the graphs that are shown and labeled (a)–(d). x^2 = - 4y

In Exercises 1–4, find the focus and directrix of each parabola with the given equation. Then match each equation to one of the graphs that are shown and labeled (a)–(d). y^2 = - 4x

Find the standard form of the equation of the ellipse satisfying the given conditions. Foci: (-4,0), (4,0); Vertices: (-5,0) (5,0)

Find the standard form of the equation of the ellipse satisfying the given conditions. Major axis horizontal with length 12; length of minor axis = 4; center: (-3,5)

Graph each ellipse and locate the foci. x²/25 +y²/64 = 1

Find the standard form of the equation of each hyperbola satisfying the given conditions. Foci: (0, −3), (0, 3) ; vertices: (0, −1), (0, 1)

Find the focus and directrix of the parabola with the given equation. Then graph the parabola. $y^2=16x$

Find the focus and directrix of the parabola with the given equation. Then graph the parabola. y² = - 8x

Find the standard form of the equation of each hyperbola satisfying the given conditions. Foci: (−4, 0), (4, 0); vertices:(−3, 0), (3, 0)

Graph each ellipse and locate the foci. x²/49 +y²/81 = 1

Find the focus and directrix of the parabola with the given equation. Then graph the parabola. x² = 12y

Graph each ellipse and locate the foci. x²/(9/4) +y²/(25/4) = 1

Find the standard form of the equation of each hyperbola satisfying the given conditions. Endpoints of transverse axis: (0, −6), (0, 6); asymptote: y=2x

Find the focus and directrix of the parabola with the given equation. Then graph the parabola. x² = - 16y

Find the standard form of the equation of each hyperbola satisfying the given conditions. Center: (4, −2); Focus: (7, −2); vertex: (6, −2)

Graph each ellipse and locate the foci. x² = 1 – 4y²

Use vertices and asymptotes to graph each hyperbola. Locate the foci and find the equations of the asymptotes. x²/9−y²/25=1

Graph each ellipse and locate the foci. 25x²+4y² = 100

Find the focus and directrix of the parabola with the given equation. Then graph the parabola. y² - 6x = 0

Find the focus and directrix of the parabola with the given equation. Then graph the parabola. 8x² + 4y = 0

In Exercises 13–26, use vertices and asymptotes to graph each hyperbola. Locate the foci and find the equations of the asymptotes. x²/100−y²/64=1