 Back
BackProblem 25
Solve each system of equations using matrices. Use Gaussian elimination with back-substitution or Gauss-Jordan elimination.
Problem 25
In Exercises 23–30, use expansion by minors to evaluate each determinant.
Problem 27
Solve each system of equations using matrices. Use Gaussian elimination with back-substitution or Gauss-Jordan elimination.
Problem 27
In Exercises 23–30, use expansion by minors to evaluate each determinant.
Problem 27ab
In Exercises 27 - 36, find (if possible) the following matrices: a. AB b. BA 1 3 3 - 2 A = B = 5 3 - 1 6
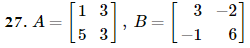
Problem 28
Solve for X in the matrix equation 3X+A = B where
Problem 29
Write each linear system as a matrix equation in the form AX = B, where A is the coefficient matrix and B is the constant matrix.
Problem 29
In Exercises 23–30, use expansion by minors to evaluate each determinant.
Problem 29
Solve each system of equations using matrices. Use Gaussian elimination with back-substitution or Gauss-Jordan elimination.
Problem 29ab
In Exercises 27 - 36, find (if possible) the following matrices: a. AB b. BA 1 2 A = [1 2 3 4], B = 3 4

Problem 31
Write each linear system as a matrix equation in the form AX = B, where A is the coefficient matrix and B is the constant matrix.
Problem 31
Solve each system of equations using matrices. Use Gaussian elimination with back-substitution or Gauss-Jordan elimination.
Problem 31
In Exercises 31–36, use the alternative method for evaluating third-order determinants on here to evaluate each determinant.
Problem 31ab
In Exercises 27 - 36, find (if possible) the following matrices: a. AB b. BA 1 - 1 4 1 1 0 A = 4 - 1 3 B = 1 2 4 2 0 - 2 1 - 1 3

Problem 33
In Exercises 31–36, use the alternative method for evaluating third-order determinants on here to evaluate each determinant.
Problem 33
Solve each system of equations using matrices. Use Gaussian elimination with back-substitution or Gauss-Jordan elimination.
Problem 33
Write each matrix equation as a system of linear equations without matrices.
Problem 33ab
In Exercises 27 - 36, find (if possible) the following matrices: a. AB b. BA 4 2 2 3 4 A = 6 1 B = 3 5 - 1 - 2 0

Problem 35
Solve each system of equations using matrices. Use Gaussian elimination with back-substitution or Gauss-Jordan elimination.
Problem 35
In Exercises 31–36, use the alternative method for evaluating third-order determinants on here to evaluate each determinant.
Problem 35
Write each matrix equation as a system of linear equations without matrices.
Problem 35ab
In Exercises 27 - 36, find (if possible) the following matrices: a. AB b. BA 1 2 2 - 3 1 - 1 - 1 1 A = B = 1 1 - 2 1 5 4 10 5
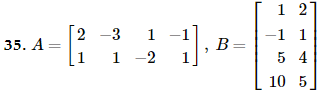
Problem 37
a. Write each linear system as a matrix equation in the form AX = B. b. Solve the system using the inverse that is given for the coefficient matrix.
Problem 37
In Exercises 37–44, use Cramer's Rule to solve each system.
Problem 37
Perform the indicated matrix operations given that A, B and C are defined as follows. If an operation is not defined, state the reason.
4B - 3C
Problem 37
Solve each system of equations using matrices. Use Gaussian elimination with back-substitution or Gauss-Jordan elimination.
Problem 37
In Exercises 37–38, find the products and to determine whether B is the multiplicative inverse of A.
Problem 39
a. Write each linear system as a matrix equation in the form AX = B. b. Solve the system using the inverse that is given for the coefficient matrix.
Problem 39
In Exercises 37–44, use Cramer's Rule to solve each system.
Problem 39
Find the quadratic function f(x) = ax² + bx + c for which ƒ( − 2) = −4, ƒ(1) = 2, and f(2) = 0.
