Solve each logarithmic equation in Exercises 49–92. Be sure to reject any value of x that is not in the domain of the original logarithmic expressions. Give the exact answer. Then, where necessary, use a calculator to obtain a decimal approximation, correct to two decimal places, for the solution. log₄(x+5)=3

Use properties of logarithms to condense each logarithmic expression. Write the expression as a single logarithm whose coefficient is 1. Where possible, evaluate logarithmic expressions without using a calculator. 2 log_b x + 3 log_b y

Begin by graphing f(x) = log₂ x. Then use transformations of this graph to graph the given function. What is the vertical asymptote? Use the graphs to determine each function's domain and range. g(x) = log₂ (x + 1)

Use the compound interest formulas A = P (1+ r/n)^nt and A =Pe^rt to solve exercises 53-56. Round answers to the nearest cent. Find the accumulated value of an investment of $10,000 for 5 years at an interest rate of 1.32% if the money is a. compounded semiannually

Use the compound interest formulas A = P (1+ r/n)^nt and A =Pe^rt to solve exercises 53-56. Round answers to the nearest cent. Find the accumulated value of an investment of $10,000 for 5 years at an interest rate of 1.32% if the money is b. compounded quarterly

Use the compound interest formulas A = P (1+ r/n)^nt and A =Pe^rt to solve exercises 53-56. Round answers to the nearest cent. Find the accumulated value of an investment of $10,000 for 5 years at an interest rate of 1.32% if the money is c. compounded monthly.

Use the compound interest formulas A = P (1+ r/n)^nt and A =Pe^rt to solve exercises 53-56. Round answers to the nearest cent. Find the accumulated value of an investment of $10,000 for 5 years at an interest rate of 1.32% if the money is d. compounded continuously.

In Exercises 54–57, use properties of logarithms to condense each logarithmic expression. Write the expression as a single logarithm whose coefficient is $1$. $\log 3-3\log x$

Use the compound interest formulas A = P (1+ r/n)^nt and A =Pe^rt to solve exercises 53-56. Round answers to the nearest cent. Suppose that you have $12,000 to invest. Which investment yields the greater return over 3 years: 0.96% compounded monthly or 0.95% compounded continuously?

Use properties of logarithms to condense each logarithmic expression. Write the expression as a single logarithm whose coefficient is 1. Where possible, evaluate logarithmic expressions without using a calculator. 5 ln x - 2 ln y

Begin by graphing f(x) = log₂ x. Then use transformations of this graph to graph the given function. What is the vertical asymptote? Use the graphs to determine each function's domain and range. h(x)=1+ log₂ x

Solve each logarithmic equation in Exercises 49–92. Be sure to reject any value of x that is not in the domain of the original logarithmic expressions. Give the exact answer. Then, where necessary, use a calculator to obtain a decimal approximation, correct to two decimal places, for the solution. log₂(x+25)=4

Begin by graphing f(x) = log₂ x. Then use transformations of this graph to graph the given function. What is the vertical asymptote? Use the graphs to determine each function's domain and range. h(x) = 2 + log₂x

Solve each logarithmic equation in Exercises 49–92. Be sure to reject any value of x that is not in the domain of the original logarithmic expressions. Give the exact answer. Then, where necessary, use a calculator to obtain a decimal approximation, correct to two decimal places, for the solution. log₃(x+4)=−3

Use properties of logarithms to condense each logarithmic expression. Write the expression as a single logarithm whose coefficient is 1. (1/2)ln x - ln y

In Exercises 53-58, begin by graphing f(x) = log₂ x. Then use transformations of this graph to graph the given function. What is the vertical asymptote? Use the graphs to determine each function's domain and range. g(x) = (1/2)log₂ x

Graph f and g in the same rectangular coordinate system. Then find the point of intersection of the two graphs. f(x) = 2^x, g(x) = 2^-x

Use properties of logarithms to condense each logarithmic expression. Write the expression as a single logarithm whose coefficient is 1. Where possible, evaluate logarithmic expressions without using a calculator. 3 ln x - (1/3) ln y

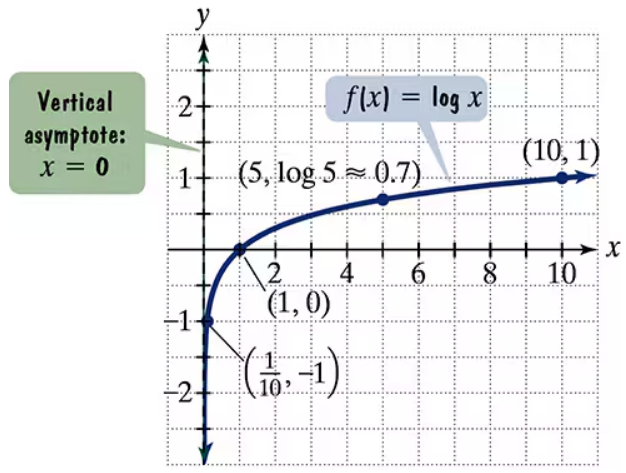
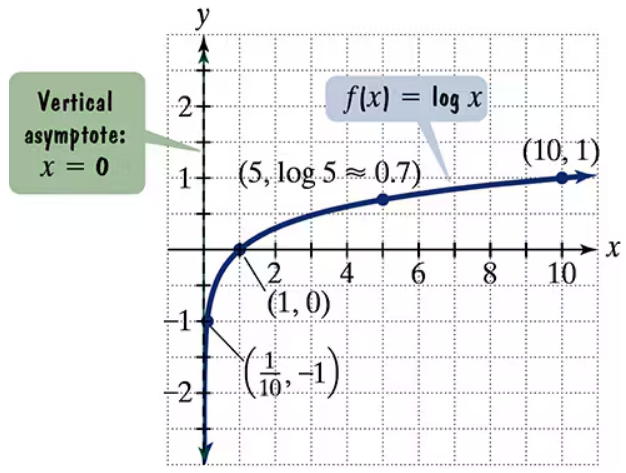
The figure shows the graph of f(x) = log x. In Exercises 59–64, use transformations of this graph to graph each function. Graph and give equations of the asymptotes. Use the graphs to determine each function's domain and range. g(x) = log(x − 1)

Solve each logarithmic equation in Exercises 49–92. Be sure to reject any value of x that is not in the domain of the original logarithmic expressions. Give the exact answer. Then, where necessary, use a calculator to obtain a decimal approximation, correct to two decimal places, for the solution. log₄(3x+2)=3

Use properties of logarithms to condense each logarithmic expression. Write the expression as a single logarithm whose coefficient is 1. Where possible, evaluate logarithmic expressions without using a calculator. 4 ln (x + 6) - 3 ln x

In Exercises 58–59, use common logarithms or natural logarithms and a calculator to evaluate to four decimal places. log₄ 0.863

Graph y= 2^x and x = 2^y in the same rectangular coordinate system.

In Exercises 60–63, determine whether each equation is true or false. Where possible, show work to support your conclusion. If the statement is false, make the necessary change(s) to produce a true statement. (ln x)(ln 1) = 0

Solve each logarithmic equation in Exercises 49–92. Be sure to reject any value of x that is not in the domain of the original logarithmic expressions. Give the exact answer. Then, where necessary, use a calculator to obtain a decimal approximation, correct to two decimal places, for the solution. 5 ln(2x)=20

Use properties of logarithms to condense each logarithmic expression. Write the expression as a single logarithm whose coefficient is 1. Where possible, evaluate logarithmic expressions without using a calculator. 3 ln x + 5 ln y - 6 ln z

The figure shows the graph of f(x) = log x. In Exercises 59–64, use transformations of this graph to graph each function. Graph and give equations of the asymptotes. Use the graphs to determine each function's domain and range. h(x) = log x − 1

Give the equation of each exponential function whose graph is shown.

In Exercises 60–63, determine whether each equation is true or false. Where possible, show work to support your conclusion. If the statement is false, make the necessary change(s) to produce a true statement. (log2 x)^4 = 4 log2 x

Use properties of logarithms to condense each logarithmic expression. Write the expression as a single logarithm whose coefficient is 1. Where possible, evaluate logarithmic expressions without using a calculator. (1/2)(log x + log y)