Use properties of logarithms to condense each logarithmic expression. Write the expression as a single logarithm whose coefficient is 1. Where possible, evaluate logarithmic expressions without using a calculator. (1/2)(log x + log y)

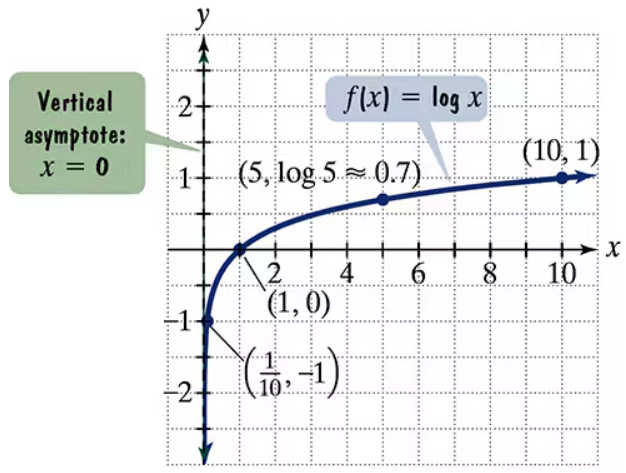
The figure shows the graph of f(x) = log x. In Exercises 59–64, use transformations of this graph to graph each function. Graph and give equations of the asymptotes. Use the graphs to determine each function's domain and range.

g(x) = 1-log x

Give the equation of each exponential function whose graph is shown.

In Exercises 64–73, solve each exponential equation. Where necessary, express the solution set in terms of natural or common logarithms and use a calculator to obtain a decimal approximation, correct to two decimal places, for the solution. 2^(4x-2) = 64

Use properties of logarithms to condense each logarithmic expression. Write the expression as a single logarithm whose coefficient is 1. Where possible, evaluate logarithmic expressions without using a calculator. $\frac{1}{2} \left( \log_5 x + \log_5 y \right) - 2 \log_5 (x + 1)$

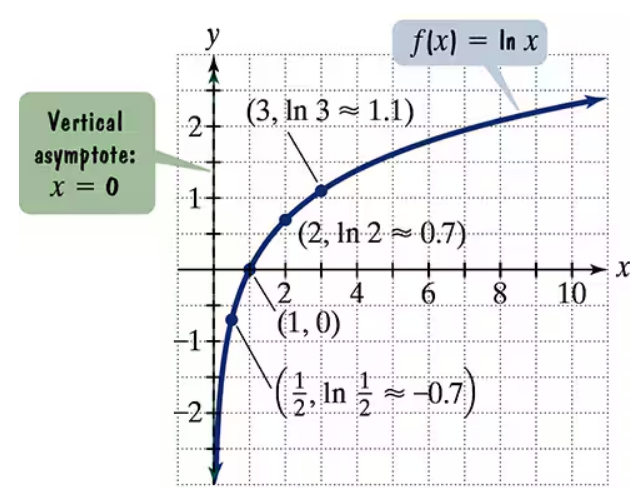
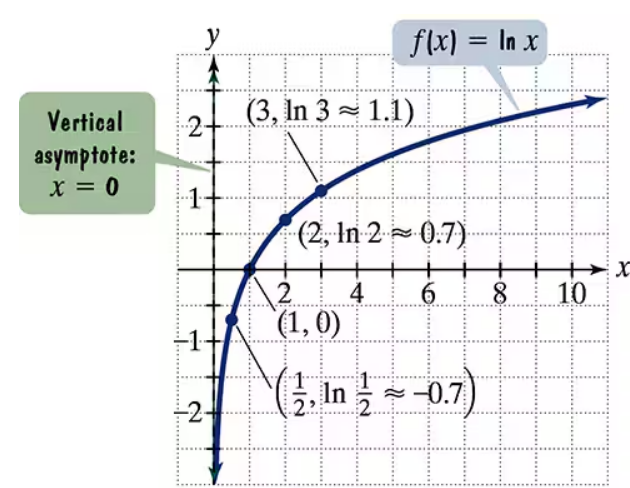
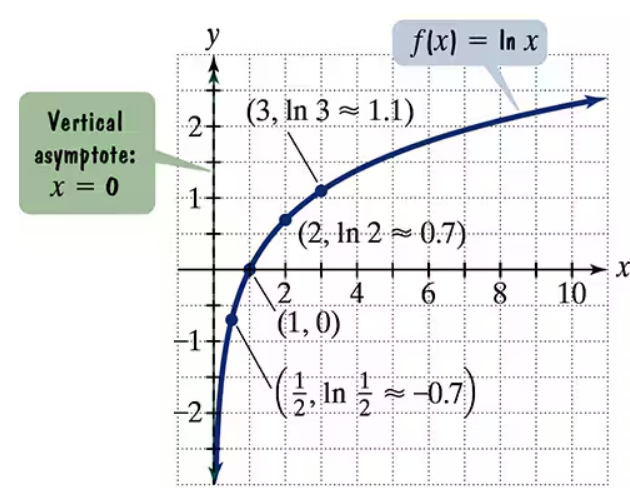
The figure shows the graph of f(x) = ln x. In Exercises 65–74, use transformations of this graph to graph each function. Graph and give equations of the asymptotes. Use the graphs to determine each function's domain and range. g(x) = ln (x+2)

Solve each logarithmic equation in Exercises 49–92. Be sure to reject any value of $x$ that is not in the domain of the original logarithmic expressions. Give the exact answer. Then, where necessary, use a calculator to obtain a decimal approximation, correct to two decimal places, for the solution. $\ln \sqrt{x+3}=1$

In Exercises 64–73, solve each exponential equation. Where necessary, express the solution set in terms of natural or common logarithms and use a calculator to obtain a decimal approximation, correct to two decimal places, for the solution. 10^x = 7000

Use properties of logarithms to condense each logarithmic expression. Write the expression as a single logarithm whose coefficient is 1. Where possible, evaluate logarithmic expressions without using a calculator. $\frac{1}{3} \left[ 2 \ln(x + 5) - \ln x - \ln (x^2 - 4) \right]$

Solve each logarithmic equation in Exercises 49–92. Be sure to reject any value of x that is not in the domain of the original logarithmic expressions. Give the exact answer. Then, where necessary, use a calculator to obtain a decimal approximation, correct to two decimal places, for the solution. log₅ x+log₅(4x−1)=1

The figure shows the graph of f(x) = ln x. In Exercises 65–74, use transformations of this graph to graph each function. Graph and give equations of the asymptotes. Use the graphs to determine each function's domain and range.

h(x) = ln (2x)

The figure shows the graph of f(x) = ln x. In Exercises 65–74, use transformations of this graph to graph each function. Graph and give equations of the asymptotes. Use the graphs to determine each function's domain and range. h(x) = ln(x/2)

In Exercises 64–73, solve each exponential equation. Where necessary, express the solution set in terms of natural or common logarithms and use a calculator to obtain a decimal approximation, correct to two decimal places, for the solution. $8^x=12143$

Use properties of logarithms to condense each logarithmic expression. Write the expression as a single logarithm whose coefficient is 1. Where possible, evaluate logarithmic expressions without using a calculator. $\log x + \log(x^2 - 1) - \log 7 - \log(x + 1)$

Solve each logarithmic equation in Exercises 49–92. Be sure to reject any value of x that is not in the domain of the original logarithmic expressions. Give the exact answer. Then, where necessary, use a calculator to obtain a decimal approximation, correct to two decimal places, for the solution. log₃(x+6)+log₃(x+4)=1

The figure shows the graph of f(x) = ln x. In Exercises 65–74, use transformations of this graph to graph each function. Graph and give equations of the asymptotes. Use the graphs to determine each function's domain and range. g(x) = 2 ln x

In Exercises 71–78, use common logarithms or natural logarithms and a calculator to evaluate to four decimal places. log₅ 13

Solve each logarithmic equation in Exercises 49–92. Be sure to reject any value of x that is not in the domain of the original logarithmic expressions. Give the exact answer. Then, where necessary, use a calculator to obtain a decimal approximation, correct to two decimal places, for the solution. log₂(x+2)−log₂(x−5)=3

Solve each logarithmic equation in Exercises 49–92. Be sure to reject any value of x that is not in the domain of the original logarithmic expressions. Give the exact answer. Then, where necessary, use a calculator to obtain a decimal approximation, correct to two decimal places, for the solution. 2 log₃(x+4)=log₃ 9 + 2

In Exercises 71–78, use common logarithms or natural logarithms and a calculator to evaluate to four decimal places. log₁₄ 87.5

Solve each logarithmic equation in Exercises 49–92. Be sure to reject any value of x that is not in the domain of the original logarithmic expressions. Give the exact answer. Then, where necessary, use a calculator to obtain a decimal approximation, correct to two decimal places, for the solution. log₂(x−6)+log₂(x−4)−log₂ x=2

Find the domain of each logarithmic function. f(x) = log₅(x+4)

In Exercises 71–78, use common logarithms or natural logarithms and a calculator to evaluate to four decimal places. log_0.1 17

In Exercises 74–79, solve each logarithmic equation. log2 (x+3) + log2 (x-3) =4

Solve each logarithmic equation in Exercises 49–92. Be sure to reject any value of x that is not in the domain of the original logarithmic expressions. Give the exact answer. Then, where necessary, use a calculator to obtain a decimal approximation, correct to two decimal places, for the solution. log(x+4)=log x+log 4

Find the domain of each logarithmic function. f(x) = log (2 - x)

Use common logarithms or natural logarithms and a calculator to evaluate to four decimal places. log_π 63

Solve each logarithmic equation in Exercises 49–92. Be sure to reject any value of x that is not in the domain of the original logarithmic expressions. Give the exact answer. Then, where necessary, use a calculator to obtain a decimal approximation, correct to two decimal places, for the solution. log(3x−3)=log(x+1)+log 4

In Exercises 74–79, solve each logarithmic equation. log₄ (2x+1) = log₄ (x-3) + log₄ (x+5)

Find the domain of each logarithmic function. f(x) = ln (x-2)²