In Exercises 19–29, evaluate each expression without using a calculator. If evaluation is not possible, state the reason. ln e⁵

Begin by graphing f(x) = 2^x. Then use transformations of this graph to graph the given function. Be sure to graph and give equations of the asymptotes. Use the graphs to determine each function's domain and range. If applicable, use a graphing utility to confirm your hand-drawn graphs. g(x) = 2^x+1

Evaluate each expression without using a calculator. log₅ (1/5)

Solve each exponential equation in Exercises 23–48. Express the solution set in terms of natural logarithms or common logarithms. Then use a calculator to obtain a decimal approximation, correct to two decimal places, for the solution. e^x=5.7

Use properties of logarithms to expand each logarithmic expression as much as possible. Where possible, evaluate logarithmic expressions without using a calculator. log₆ (36/(√(x+1))

Solve each exponential equation in Exercises 23–48. Express the solution set in terms of natural logarithms or common logarithms. Then use a calculator to obtain a decimal approximation, correct to two decimal places, for the solution. 5^x=17

Begin by graphing f(x) = 2^x. Then use transformations of this graph to graph the given function. Be sure to graph and give equations of the asymptotes. Use the graphs to determine each function's domain and range. If applicable, use a graphing utility to confirm your hand-drawn graphs. g(x) = 2^x – 1

Use properties of logarithms to expand each logarithmic expression as much as possible. Where possible, evaluate logarithmic expressions without using a calculator. log_b ((x²y)/z²)

Evaluate each expression without using a calculator. log₂ (1/8)

Solve each exponential equation in Exercises 23–48. Express the solution set in terms of natural logarithms or common logarithms. Then use a calculator to obtain a decimal approximation, correct to two decimal places, for the solution. 5e^x=23

Evaluate each expression without using a calculator. log₇ √7

Use properties of logarithms to expand each logarithmic expression as much as possible. Where possible, evaluate logarithmic expressions without using a calculator. log √(100x)

Begin by graphing f(x) = 2^x. Then use transformations of this graph to graph the given function. Be sure to graph and give equations of the asymptotes. Use the graphs to determine each function's domain and range. If applicable, use a graphing utility to confirm your hand-drawn graphs. h(x) = 2^x+1 – 1

Graph f(x) = 2^x and g(x) = log2 x in the same rectangular coordinate system. Use the graphs to determine each function's domain and range.

Evaluate each expression without using a calculator. log₂ (1/√2)

Begin by graphing f(x) = 2^x. Then use transformations of this graph to graph the given function. Be sure to graph and give equations of the asymptotes. Use the graphs to determine each function's domain and range. If applicable, use a graphing utility to confirm your hand-drawn graphs. g(x) = −2^x

Solve each exponential equation in Exercises 23–48. Express the solution set in terms of natural logarithms or common logarithms. Then use a calculator to obtain a decimal approximation, correct to two decimal places, for the solution. 3e^5x=1977

Use properties of logarithms to expand each logarithmic expression as much as possible. Where possible, evaluate logarithmic expressions without using a calculator. log ∛(x/y)

Solve each exponential equation in Exercises 23–48. Express the solution set in terms of natural logarithms or common logarithms. Then use a calculator to obtain a decimal approximation, correct to two decimal places, for the solution. e^(1−5x)=793

Use properties of logarithms to expand each logarithmic expression as much as possible. Where possible, evaluate logarithmic expressions without using a calculator. ${\log }_b\left(\frac{\sqrt{x}{y}^3}{z^3}\right)$

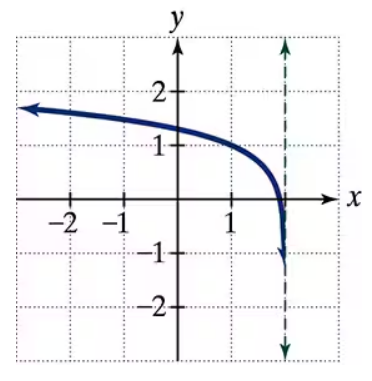
In Exercises 32–35, the graph of a logarithmic function is given. Select the function for each graph from the following options: f(x) = log x, g(x) = log(-x), h(x) = log(2-x), r(x)= 1+log(2-x)

Begin by graphing f(x) = 2^x. Then use transformations of this graph to graph the given function. Be sure to graph and give equations of the asymptotes. Use the graphs to determine each function's domain and range. If applicable, use a graphing utility to confirm your hand-drawn graphs. g(x) = 2.2^x

Evaluate each expression without using a calculator. log₆₄ 8

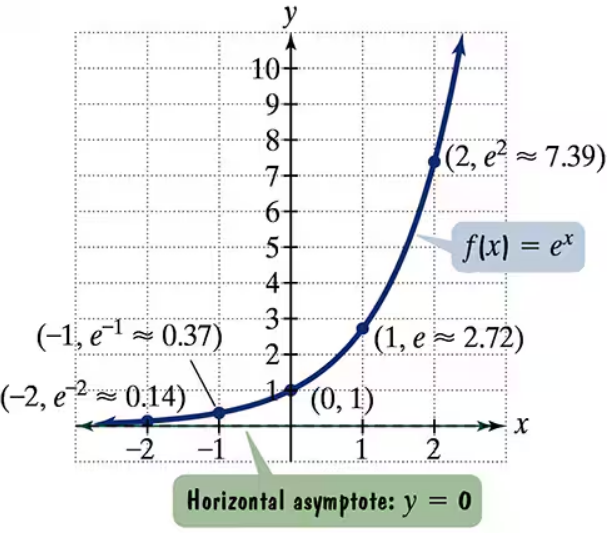
The figure shows the graph of f(x) = e^x. In Exercises 35-46, use transformations of this graph to graph each function. Be sure to give equations of the asymptotes. Use the graphs to determine graphs. each function's domain and range. If applicable, use a graphing utility to confirm your hand-drawn g(x) = e^x-1

Solve each exponential equation in Exercises 23–48. Express the solution set in terms of natural logarithms or common logarithms. Then use a calculator to obtain a decimal approximation, correct to two decimal places, for the solution. e^(5x−3) - 2 =10,476

Use properties of logarithms to expand each logarithmic expression as much as possible. Where possible, evaluate logarithmic expressions without using a calculator. $\log_5 \sqrt[3]{\frac{x^2 y}{24}}$

Evaluate each expression without using a calculator. log₅ 5

In Exercises 36–38, begin by graphing f(x) = log2 x Then use transformations of this graph to graph the given function. What is the graph's x-intercept? What is the vertical asymptote? Use the graphs to determine each function's domain and range. g(x) = log2 (x-2)

The figure shows the graph of f(x) = e^x. In Exercises 35-46, use transformations of this graph to graph each function. Be sure to give equations of the asymptotes. Use the graphs to determine graphs. each function's domain and range. If applicable, use a graphing utility to confirm your hand-drawn g(x) = e^x+2

Use properties of logarithms to expand each logarithmic expression as much as possible. Where possible, evaluate logarithmic expressions without using a calculator. $\ln \left( \frac{x^3 \sqrt{x^2 + 1}}{(x + 1)^4} \right)$