Find ƒ+g and determine the domain for each function. f(x)= = 8x/(x - 2), g(x) = 6/(x+3)

In Exercises 39-52, a. Find an equation for ƒ¯¹(x). b. Graph ƒ and ƒ¯¹(x) in the same rectangular coordinate system. c. Use interval notation to give the domain and the range off and ƒ¯¹. f(x) = x³ − 1

Find f−g and determine the domain for each function. f(x)= = 8x/(x - 2), g(x) = 6/(x+3)

Find fg and determine the domain for each function. f(x)= = 8x/(x - 2), g(x) = 6/(x+3)

Find f/g and determine the domain for each function. f(x)= = 8x/(x - 2), g(x) = 6/(x+3)

Solve: 2x^2/3 - 5x^1/3 -3 = 0.

In Exercises 46–49, give the slope and y-intercept of each line whose equation is given. Then graph the line. y = (2/5)x - 1

In Exercises 39–50, graph the given functions, f and g, in the same rectangular coordinate system. Select integers for x, starting with -2 and ending with 2. Once you have obtained your graphs, describe how the graph of g is related to the graph of f. f(x)= |x|, g(x) = |x| +1

Give the slope and y-intercept of each line whose equation is given. Then graph the linear function. y = -2x/5+6

Find ƒ+g, f−g, fg, and f/g. Determine the domain for each function. f(x)= = 9x/(x - 4), g(x) = 7/(x+8)

Give the center and radius of the circle described by the equation and graph each equation. Use the graph to identify the relation's domain and range. (x + 2)² + (y + 2)² = 4

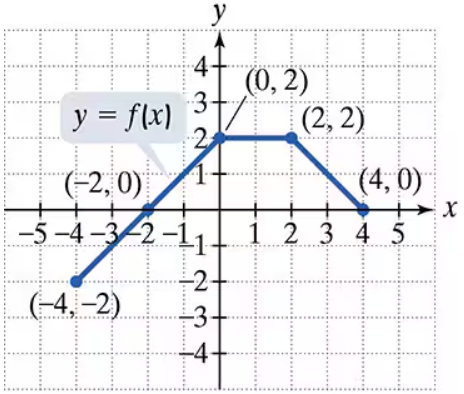
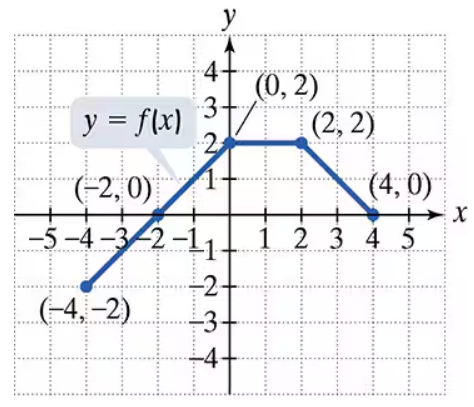
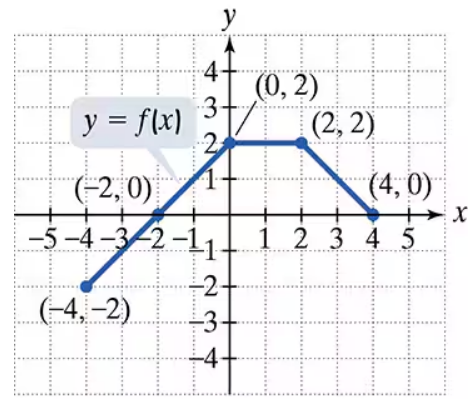
Use the graph of y = f(x) to graph each function g. g(x) = -f(x-1) + 1

Find ƒ+g and determine the domain for each function. f(x) = √(x +4), g(x) = √(x − 1)

In Exercises 39–50, graph the given functions, f and g, in the same rectangular coordinate system. Select integers for x, starting with -2 and ending with 2. Once you have obtained your graphs, describe how the graph of g is related to the graph of f. f(x) = x³, g(x) = x³ +2

In Exercises 39-52, a. Find an equation for ƒ¯¹(x). b. Graph ƒ and ƒ¯¹(x) in the same rectangular coordinate system. c. Use interval notation to give the domain and the range off and ƒ¯¹. f(x) = (x+2)³

In Exercises 31–50, find f−g and determine the domain for each function. f(x) = √(x +4), g(x) = √(x − 1)

In Exercises 31–50, find fg and determine the domain for each function. f(x) = √(x +4), g(x) = √(x − 1)

In Exercises 31–50, find f/g and determine the domain for each function. f(x) = √(x +4), g(x) = √(x − 1)

Use the graph of y = f(x) to graph each function g. g(x) = -f(x + 1) − 1

In Exercises 46–49, give the slope and y-intercept of each line whose equation is given. Then graph the line. 2x + 3y + 6 = 0

In Exercises 41–52, give the center and radius of the circle described by the equation and graph each equation. Use the graph to identify the relation's domain and range. x² + (y − 1)² = 1

Graph each equation in a rectangular coordinate system. y = -2

Find ƒ+g, f−g, fg, and f/g. Determine the domain for each function. f(x) = √(x -2), g(x) = √(2-x)

In Exercises 39-52, a. Find an equation for ƒ¯¹(x). b. Graph ƒ and ƒ¯¹(x) in the same rectangular coordinate system. c. Use interval notation to give the domain and the range off and ƒ¯¹. f(x) = √(x-1)

In Exercises 31–50, find ƒ+g, f−g, fg, and f/g. Determine the domain for each function. f(x) = √(x -2), g(x) = √(2-x)

In Exercises 31–50, find ƒ+g, f−g, fg, and f/g. Determine the domain for each function. f(x) = √(x -2), g(x) = √(2-x)

In Exercises 31–50, find ƒ+g, f−g, fg, and f/g. Determine the domain for each function. f(x) = √(x -2), g(x) = √(2-x)

Graph using intercepts: 2x - 5y - 10 = 0

Use the graph of y = f(x) to graph each function g. g(x) =(1/2) f(2x)

Give the center and radius of the circle described by the equation and graph each equation. Use the graph to identify the relation's domain and range. (x + 1)² + y² = 25