Multiple Choice
Based on the graph of , describe where the derivative curve would be below the x-axis.
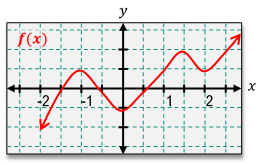
Above the x-axis
Below the x-axis
On the x-axis
 Verified step by step guidance
Verified step by step guidance
 6:15m
6:15mMaster Graphing The Derivative with a bite sized video explanation from Patrick
Start learning
