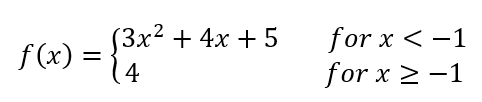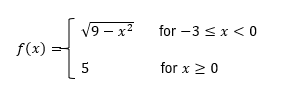Continuity: Videos & Practice Problems

Continuity in mathematics refers to the behavior of a function at a specific point. A function is considered continuous at a point c if the limit of the function as x approaches c equals the function's value at that point. In mathematical terms, this can be expressed as:

$$\lim_{{x \to c}} f(x) = f(c)$$

When both sides of this equation are equal, the function is continuous at c. Conversely, if the limit does not equal the function value, the function is discontinuous at that point.

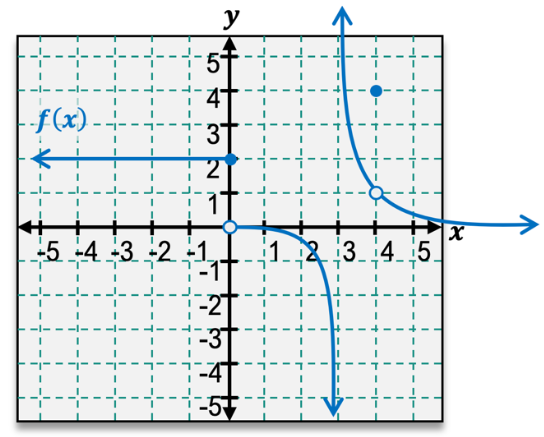
To visually assess continuity, one can trace the graph of the function. If you can draw through the point without lifting your pencil, the function is continuous there. If you must lift your pencil, it indicates a discontinuity. For example, if a function has a hole at x = 2, the limit may approach a certain value, but the function value is undefined, indicating discontinuity.

Discontinuities can arise from various situations, including:

• Holes in the graph
• Jump discontinuities, where the function abruptly changes value
• Asymptotes, where the function approaches infinity or negative infinity

Rational functions and piecewise functions frequently exhibit these types of discontinuities. For instance, consider the following examples to determine continuity:

1. For c = -2, if the limit as x approaches -2 from both sides equals the function value at -2, the function is continuous.

2. For c = 4, if the left-hand limit and right-hand limit do not match, the limit does not exist, indicating a jump discontinuity.

3. For c = 1, if the limit approaches negative infinity and the function value is undefined due to an asymptote, the function is discontinuous.

Understanding these concepts allows for a deeper comprehension of function behavior and the identification of continuity and discontinuity in various mathematical contexts.

To determine the intervals of continuity for a function, we analyze its graph from left to right, identifying points where the function is discontinuous. A function is continuous over an interval if it does not have any breaks, jumps, or asymptotes within that interval.

Starting from negative infinity, if the function extends continuously until a point of discontinuity at \( x = 0 \), we express this interval in interval notation as \( (-\infty, 0] \). The square bracket indicates that the function is continuous up to and including \( x = 0 \).

Next, we observe the behavior of the function after \( x = 0 \). If there is an open circle at this point, it signifies that the function does not include \( x = 0 \) itself, leading us to the next interval from \( 0 \) to \( x = 3 \), which is represented as \( (0, 3) \). The parenthesis indicates that \( x = 3 \) is not included due to the presence of an asymptote at this point.

Continuing from \( x = 3 \), we again find that the function resumes at this point but does not include it, so we denote this interval as \( (3, 4) \). The open circle at \( x = 4 \) indicates that this point is also not included in the interval.

Finally, as we move beyond \( x = 4 \), the function continues to positive infinity. Thus, the last interval of continuity is expressed as \( (4, \infty) \), where the parenthesis indicates that the function does not reach \( x = 4 \) itself.

In summary, the intervals of continuity for the function are:

1. \( (-\infty, 0] \)

2. \( (0, 3) \)

3. \( (3, 4) \)

4. \( (4, \infty) \)

These intervals collectively represent the regions where the function is continuous, while the points of discontinuity are located at \( x = 0 \), \( x = 3 \), and \( x = 4 \).

To determine the intervals where the function \( f(x) = \sqrt{2x - 1} \) is continuous, we first need to identify the domain of the function. The expression under the square root, \( 2x - 1 \), must be non-negative for the function to be defined. This leads us to the inequality:

\( 2x - 1 \geq 0 \)

Solving this inequality gives:

\( 2x \geq 1 \)

\( x \geq 0.5 \)

Thus, the function is defined and continuous for all \( x \) values starting from \( 0.5 \) and extending to infinity. In interval notation, this is expressed as:

\( [0.5, \infty) \)

Here, the square bracket indicates that the interval includes the endpoint \( 0.5 \), while the parenthesis for infinity indicates that it does not include infinity itself. Therefore, the function \( f(x) = \sqrt{2x - 1} \) is continuous on the interval \( [0.5, \infty) \).

Understanding the continuity of a function is crucial in calculus, especially when you are not provided with a graph. Discontinuities can arise in various forms, such as jumps, holes, or asymptotes, particularly in rational and piecewise functions. To identify where a function is discontinuous, we can follow a systematic approach.

For rational functions, the key to finding discontinuities lies in the denominator. A rational function is expressed as the ratio of two polynomials, and it is continuous everywhere except where the denominator equals zero. For example, consider the function:

$$f(x) = \frac{x^2 - x - 6}{x + 2}$$

Here, the denominator is \(x + 2\). Setting this equal to zero gives:

$$x + 2 = 0 \implies x = -2$$

This indicates a potential discontinuity at \(x = -2\). To determine the type of discontinuity, we can check if the numerator can be factored to cancel with the denominator. If it can, we have a removable discontinuity (a hole); if not, we have an asymptote.

Next, we can analyze piecewise functions for discontinuities. For instance, consider the piecewise function defined as:

$$f(x) = \begin{cases} 4 & \text{if } x < -1 \\ x + 1 & \text{if } x \geq -1 \end{cases}$$

To check for discontinuities, we focus on the point where the pieces meet, which is \(x = -1\). We need to evaluate the limit as \(x\) approaches \(-1\) from both sides and compare it to the function value at that point.

Calculating the left-sided limit:

$$\lim_{x \to -1^-} f(x) = 4$$

Calculating the right-sided limit:

$$\lim_{x \to -1^+} f(x) = -1 + 1 = 0$$

Since the left-sided limit (4) does not equal the right-sided limit (0), the overall limit does not exist at \(x = -1\). The function value at this point is:

$$f(-1) = -1 + 1 = 0$$

Since the limit does not exist and does not equal the function value, we confirm a discontinuity at \(x = -1\), specifically a jump discontinuity, as the function cannot be traced without lifting the pen.

In summary, to determine where a function is discontinuous, check the denominator for rational functions and evaluate limits for piecewise functions at the points where the pieces meet. This methodical approach will help identify and classify discontinuities effectively.

To determine the points of discontinuity for the function \( f(x) = \frac{x - 3}{x^2 + 2x - 15} \), we focus on the denominator, as discontinuities in rational functions occur where the denominator equals zero. Thus, we set the denominator \( x^2 + 2x - 15 \) to zero.

To solve this quadratic equation, we can factor it. We need to find two numbers that multiply to \(-15\) (the constant term) and add to \(2\) (the coefficient of the linear term). The numbers that satisfy these conditions are \(-3\) and \(5\). Therefore, we can factor the quadratic as:

\( (x - 3)(x + 5) = 0 \)

Setting each factor equal to zero gives us the potential points of discontinuity:

\( x - 3 = 0 \) leads to \( x = 3 \)

\( x + 5 = 0 \) leads to \( x = -5 \)

Thus, the function is discontinuous at \( x = 3 \) and \( x = -5 \).

Examining the nature of these discontinuities, we note that \( x = 3 \) corresponds to a removable discontinuity (or a hole) because the factor \( x - 3 \) in the numerator cancels with the denominator. Conversely, \( x = -5 \) represents a vertical asymptote, indicating a non-removable discontinuity since the factor \( x + 5 \) does not cancel out.

In summary, the function \( f(x) \) is discontinuous at \( x = 3 \) (removable discontinuity) and \( x = -5 \) (vertical asymptote).

To determine the points of discontinuity in a piecewise function, we need to analyze the transition points between the different pieces of the function. In this case, we focus on two critical values: \( x = -2 \) and \( x = 0 \).

Starting with \( x = -2 \), we evaluate the left-sided and right-sided limits. The left-sided limit as \( x \) approaches \(-2\) is derived from the first piece of the function, yielding:

\[\lim_{{x \to -2^-}} f(x) = 5\]

For the right-sided limit, we use the second piece of the function, which is defined as \( x^2 + 2x + 1 \). Plugging in \(-2\) gives:

\[\lim_{{x \to -2^+}} f(x) = (-2)^2 + 2(-2) + 1 = 4 - 4 + 1 = 1\]

Since the left-sided limit (5) and the right-sided limit (1) are not equal, the overall limit does not exist at \( x = -2 \). Additionally, the function value at this point, \( f(-2) = 1 \), does not match the left-sided limit. Therefore, there is a discontinuity at \( x = -2 \).

Next, we examine \( x = 0 \). Again, we calculate the left-sided and right-sided limits. The left-sided limit as \( x \) approaches \( 0 \) is:

\[\lim_{{x \to 0^-}} f(x) = 0^2 + 2(0) + 1 = 1\]

For the right-sided limit, we use the last piece of the function, which is \( x + 1 \). Thus, we find:

\[\lim_{{x \to 0^+}} f(x) = 0 + 1 = 1\]

Both the left-sided limit and the right-sided limit equal 1, indicating that the overall limit as \( x \) approaches \( 0 \) is also 1:

\[\lim_{{x \to 0}} f(x) = 1\]

Now, we check the function value at this point:

\[f(0) = 0^2 + 2(0) + 1 = 1\]

Since the limit and the function value are equal, the function is continuous at \( x = 0 \).

In conclusion, the only point of discontinuity in this piecewise function is at \( x = -2 \). The function is continuous at \( x = 0 \).