Introduction to Limits: Videos & Practice Problems

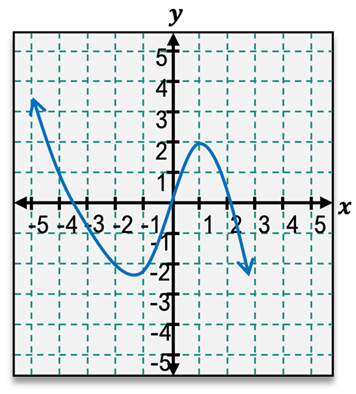
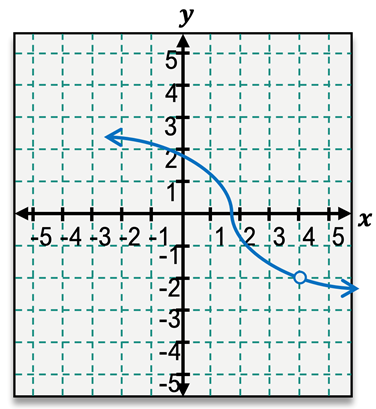
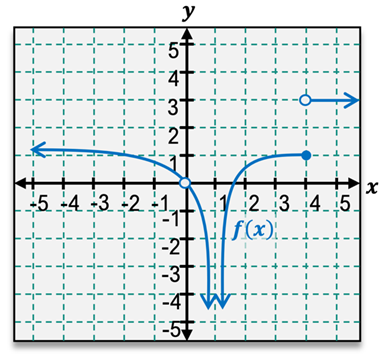
Limits are fundamental concepts in calculus that help us understand the behavior of functions as they approach a specific value. When we talk about limits, we are interested in what a function is doing around a certain value of \( x \), rather than at that exact point. This can be visualized through graphs or analyzed using tables of values.

The notation for limits is typically expressed as \( \lim_{{x \to c}} f(x) \), which reads as "the limit of \( f(x) \) as \( x \) approaches \( c \)." For example, to find the limit of \( f(x) = x^2 \) as \( x \) approaches 2, we examine the values of \( f(x) \) as \( x \) gets very close to 2 from both the left and the right. As \( x \) approaches 2, \( f(x) \) approaches 4, indicating that \( \lim_{{x \to 2}} x^2 = 4 \).

To find limits, we can use numerical methods by substituting values close to \( c \). For instance, substituting values like 1.99 and 1.999 into \( f(x) = x^2 \) yields results that approach 4. Similarly, approaching from the right with values like 2.01 and 2.001 also leads to results that converge to 4. This consistency from both sides confirms the limit.

In another example, to find the limit of \( f(x) = x + 4 \) as \( x \) approaches 1, we can create a table of values. By evaluating \( f(x) \) at values like 0.99 and 0.999, we find that \( f(x) \) approaches 5. Checking values from the right, such as 1.01 and 1.001, also confirms that the limit is 5. Interestingly, in this case, plugging in \( x = 1 \) directly gives the same result, but this is not always the case.

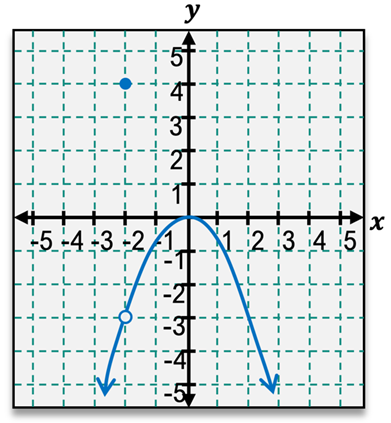
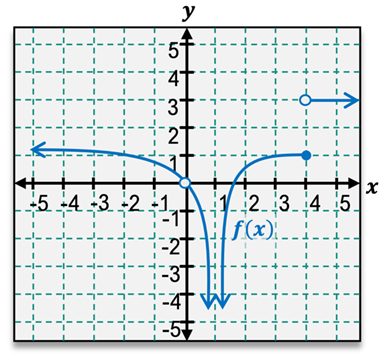
It is crucial to understand that the limit may not equal the function value at \( c \). For example, if we analyze a function \( f(x) \) as \( x \) approaches 3 using a graph, we might find that the limit is 1, even if the function value at \( x = 3 \) is 4. This discrepancy highlights the importance of examining the behavior of the function around the point rather than at the point itself.

In summary, limits provide a way to analyze the behavior of functions as they approach specific values, using both graphical and numerical methods. Understanding this concept is essential for further studies in calculus and mathematical analysis.

In analyzing limits using a graph, it's essential to observe the behavior of the function as the input approaches a specific value from both the left and right sides. For instance, when determining the limit of \( f(x) \) as \( x \) approaches \(-2\), we find that the function approaches a value of \( 1 \) from both directions. Therefore, we conclude that:

\[ \lim_{{x \to -2}} f(x) = 1 \]

Next, we examine the limit of \( f(x) \) as \( x \) approaches \( 0 \). Despite a hole in the graph at this point, the function approaches \( 0 \) from both sides. This reinforces the concept that the limit focuses on the behavior near the point, not the actual value at that point. Thus, we have:

\[ \lim_{{x \to 0}} f(x) = 0 \]

Finally, when considering the limit of \( f(x) \) as \( x \) approaches \( 3 \), the function again approaches \( 1 \) from both sides, leading to the conclusion:

\[ \lim_{{x \to 3}} f(x) = 1 \]

However, as we approach \( 4 \), we encounter a situation where the left-hand limit and right-hand limit do not agree. This discrepancy indicates that the limit does not exist at that point, highlighting the importance of checking both sides when evaluating limits. Understanding these concepts is crucial for mastering the behavior of functions and their limits in calculus.

When determining the limit of a function as the variable approaches a specific value, we focus on the y-value that the function approaches as x gets very close to that value from either side. This process involves evaluating one-sided limits, which are expressed using specific notation. For the left-sided limit, we denote it as \(\lim_{{x \to c^-}} f(x)\), indicating that x approaches c from the left. Conversely, the right-sided limit is denoted as \(\lim_{{x \to c^+}} f(x)\), indicating that x approaches c from the right. A helpful way to remember this is that x-values approaching from the left are negative, while those from the right are positive.

To illustrate, consider a piecewise function where we evaluate the left-sided limit as x approaches 3. Observing the graph, we find that as x approaches 3 from the left, the function approaches a y-value of 1. By substituting values like 2.99 and 2.999 into the function, we confirm that the left-sided limit is indeed 1: \(\lim_{{x \to 3^-}} f(x) = 1\).

Next, we evaluate the right-sided limit as x approaches 3. The graph shows that as x approaches 3 from the right, the function approaches a y-value of 4. Substituting values such as 3.01 and 3.001 into the function, we find that the right-sided limit is 4: \(\lim_{{x \to 3^+}} f(x) = 4\).

When asked to find the overall limit as x approaches 3, we note that the left-sided limit (1) and the right-sided limit (4) are not equal. This discrepancy indicates that the limit does not exist, abbreviated as DNE: \(\lim_{{x \to 3}} f(x) \text{ DNE}\).

In another example, we evaluate the limit as x approaches 1. The left-sided limit is found to be -1, and similarly, the right-sided limit is also -1. Since both one-sided limits are equal, we conclude that the overall limit exists and is equal to -1: \(\lim_{{x \to 1}} f(x) = -1\).

In summary, when working with one-sided limits, if the left-sided and right-sided limits are not equal, the overall limit does not exist. However, if they are equal, the overall limit exists and is equal to that common value. This understanding is crucial for analyzing the behavior of functions at specific points.

Understanding when a limit does not exist is crucial in calculus, as it helps in analyzing the behavior of functions. There are several scenarios where limits fail to exist, and recognizing these can enhance your problem-solving skills.

One common case occurs with piecewise functions that exhibit a jump discontinuity. For instance, consider the limit of a function \( f(x) \) as \( x \) approaches 3. If the function approaches a value of 1 from the left and a value of 4 from the right, the limit does not exist because the left-hand limit and right-hand limit are not equal. This discontinuity indicates that the function jumps from one value to another, which is a typical characteristic of piecewise functions.

Another scenario involves unbounded behavior, particularly with rational functions that have vertical asymptotes. For example, if we examine the limit of \( f(x) \) as \( x \) approaches 2 and find that the function approaches infinity from both sides, we conclude that the limit does not exist. This is because infinity is not a finite number, and thus, we cannot assign a limit value in this case. It is important to note that while we may describe the behavior of the function as approaching positive or negative infinity, this does not imply that a limit exists.

Lastly, limits can also fail to exist due to oscillation. For instance, if we analyze the limit of \( f(x) \) as \( x \) approaches 0 and observe that the function oscillates wildly, such as in the case of \( \sin(1/x) \) or \( \cos(1/x) \), the limit does not exist. Even if we zoom in on the graph, the oscillation persists, preventing us from determining a single value that the function approaches.

In summary, limits do not exist in cases of jump discontinuities, unbounded behavior, and oscillation. Recognizing these patterns is essential for effectively analyzing functions and understanding their limits.

Understanding limits is crucial in calculus, particularly when analyzing the behavior of functions as they approach specific values. In this context, we will explore how to estimate limits using graphical representations and identify when limits do not exist.

To begin, consider the limit of \( f(x) \) as \( x \) approaches \(-2\). By examining the graph, we observe that as \( x \) approaches \(-2\) from both the left and the right, the function approaches a value of \( 0 \). This indicates that the limit can be expressed as:

\[ \lim_{{x \to -2}} f(x) = 0 \]

It is important to note that the behavior of the function at values other than \(-2\) does not affect the limit at this point. The limit focuses solely on the values of \( f(x) \) as \( x \) gets infinitely close to \(-2\).

Next, we analyze the limit of \( f(x) \) as \( x \) approaches \( 0 \). Observing the graph again, we find that as \( x \) approaches \( 0 \) from both sides, the function approaches a value of \( 1 \). Thus, we can conclude:

\[ \lim_{{x \to 0}} f(x) = 1 \]

Even though there is a hole in the graph at \( x = 0 \) where the function value is actually \(-2\), this does not impact the limit since we are concerned with the behavior of the function as it approaches \( 0 \), not the value at \( 0 \).

Finally, we examine the limit of \( f(x) \) as \( x \) approaches \(-3\). The graph reveals that as \( x \) approaches \(-3\) from the left, the function approaches \( 1 \). However, from the right, the function exhibits unbounded behavior, tending towards negative infinity. This discrepancy indicates that the one-sided limits are not equal:

\[ \lim_{{x \to -3^-}} f(x) = 1 \quad \text{and} \quad \lim_{{x \to -3^+}} f(x) = -\infty \]

Since the left-hand limit and the right-hand limit do not match, we conclude that the overall limit does not exist:

\[ \lim_{{x \to -3}} f(x) \text{ does not exist} \]

In summary, when evaluating limits, it is essential to focus on the behavior of the function as it approaches the specified value, rather than the function's value at that point. This approach allows for a clearer understanding of limits, including cases where they do not exist due to unbounded behavior or differing one-sided limits.